Привет всем, кто зашел в эту тему. В ней я бы хотел рассказать вам немного об одной интересной структуре данных, а еще больше — узнать ваше мнение о ней.
Для тех, кто не знает, что это — статья на Википедии. А для тех, кто не очень любит читать много текста, перескажу в двух словах. Фильтр Блума — это вероятностная структура данных, позволяющая хранить некое множество элементов, а также быстро отвечать на запрос о том, есть ли данный элемент во множестве или нет. Вероятностная она потому что при запросе есть вероятность получить ложноположительный ответ. Почему это так? Ответ в алгоритме работы структуры. Сама структура состоит из битового массива размера m и k хэш-функций, каждая из которых для данного элемента возвращает число от 0 до m-1. Добавление элемента происходит достаточно просто — на позиции h1(e), h2(e), ..., hk(e) в массиве проставляются единицы (**hi()** — хэш-функция, е — добавляемый элемент). Как легко можно догадаться, проверка происходит аналогичным образом, считаются хэш-функции и проверяются соответствующие позиции, если на них все единицы, то элемент присутствует во множестве, в противном случае можно на 100% быть уверенным, что его там нет. Теперь ясно, почему положительный ответ на запрос не может считаться 100% верным, ведь может так получится, что для некоего элемента, которого нет в множестве, единицы на месте посчитанных значений уже проставлены в результате того, что некоторые элементы из множества для некоторых хэш-функций имеют одинаковые значения с элементом. 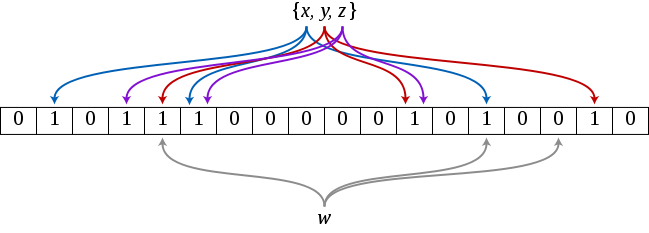
При таком подходе, вероятность, что ответ на запрос будет ложноположителен, приблизительно равна 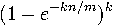 , где n — это количество элементов во множестве. Кому интересно, формула доказывается в статье на Википедии, тут мы об этом не будем.
, где n — это количество элементов во множестве. Кому интересно, формула доказывается в статье на Википедии, тут мы об этом не будем.
К чему все это. Такая структура данных может быть достаточно полезной, ведь она малоемка, проста в понимании и в реализации. Гугл, как мне известно, использует ее в своем проекте BigTable для уменьшения обращений к диску, в случае если нужного элемента нет на диске, а также в Google Chrome для опознавания вредоносных сайтов. Но может ли такая структура быть полезной в олимпиадном программировании?
Когда я недавно наткнулся на статью в Википедии, это все мне показалось очень чудесным, я обрадовался, подумал "вот, сейчас реализую эту штуку как надо, а потом буду везде юзать, ура-ура". Но затем я открыл Eclipse, написал это чудо, потестировал и был слегка разочарован в результатах.
Задачу, которую помогает решать фильтр, обычно я решаю с помощью HashSet'а, поэтому сравнивать буду именно с ним.
Я заполнял массив длинной n = 2 х 10^5 рандомными интами, после чего добавлял первую половину массива в структуру данных, а для второй половины проверял принадлежность элементов множеству.
Первоначально я выбрал m = 192937983, это достаточно большое простое число, близкое к 5 х 2^25, в Java битовый массив реализуется BitSet'ом, в котором каждая ячейка занимает 1 бит памяти, таким образом такой массив занимает 5 х 2^25 б = 20 мб памяти, и k = 20, такая величина была выбрана, потому что запрос в фильтре выполняется за O(k), а в HashSet за O(logn), и при k = 20 и n = 10^5 это примерно равные величины.
При первом тестировании я использовал лажовые хэш-функции, в результате чего получил лажовые результаты, затем я их поправил и результаты заметно улучшились, ниже уже поправленная версия результатов.
Для таких параметров m, k, n я получил вероятность ложного срабатывания p = 1e-40, подумал, что это достаточно неплохо и я могу рассчитывать на хорошие результаты. И действительно, фильтр на 20 тестов не делал ни одной ошибки, что вполне похвально. Только вот время мне не нравилось — фильтр работал в 5-6 раз медленнее, чем HashSet. Для того, чтобы он работал быстрее, пришлось уменьшить m до 10^7 и k до 5. Но теперь на эти же самые 20 тестов в среднем получалось по 10 ошибок, что уже не есть очень хорошо.
В общем, я получил в результате не то, что ожидал, я надеялся, что смогу эффективно заменить HashSet на эту штуку, но этому не бывать, к сожалению, ведь эту структуру нельзя заставить работать и быстро и точно одновременно, только одно из двух.
А теперь я хочу вас спросить, жители Codeforces, может ли пригодиться эта структура данных в олимпиадном программировании, хоть где-нибудь, и пусть даже не структура, а сама идея структуры? В общем, может кто-нибудь уже что-нибудь такое делал, или слышал, или придумал, расскажите, мне очень интересно будет почитать.
Пока слышал только о том, что с помощью фильтра можно оптимизировать работу хэш-мапы, ну, ясно, как это делается.











Структура, конечно, довольно интересная. Проблема в следующем: в олимпиадном программировании не используются структуры данных, доступ к которым мы можем назвать дорогим. Извиняюсь, сетевой запрос с латентностью даже 10мс переплюнет что угодно из используемого в СП.
Насчет идеи: см. перебор с отсечением и все, что ему родственно :).
Смежный вопрос: кто-нибудь пробовал реализовать Perfect Hash или Cuckoo Hash и порвать HashSet?
У тебя
хуплохие хеш-функции.вот код, эмулирующий хорошие хэш-функции, который при заданных параметрах не даёт ни одной ошибки.
PS: я ошибся, что ошибся, потому правок километр.
Да, все так, сам некоторое время назад придумал нормальные хэш-функции, с которыми все боле-мене нормально работает, так что сейчас отредактирую.
Запрос в HashSet выполняется не за O(log n), а за ожидаемое время O(1).
Благодаря этой теме, узнал для себя пару интересных вещей, спасибо. Глянул реализацию HashSet в Java 6, и что меня немного удивило, он реализован на HashMap'е. Глянул же реализацию HashMap, и действительно, запрос происходит в лучшем случае за O(1), хотя в среднем там будет какая-то совсем маленькая константа.
Еще вот это прочитай: http://codeforces.me/blog/entry/4876 :)
Так я правильно понимаю, что смысл этой структуры не в быстродействии а в компактности хранения? (ну т.е. в том чтобы хранить состояние множества из потенциальных N элементов в меньше чем N битах)
Не, чепуху спросил. Мы собираемся хранить множество из потенциальных N элементов, однако при условии что в нём по жизни будет N'<<N элементов, и даже N'<<M... И вот для такого хранения мы хотим добиться какого-то быстродействия... М-да... При таком количестве операций состязаться с HashMap трудновато будет... если только в том не оч много коллизий при текущем размере таблицы и выбранной хеш-функции... %)
О, ну вот зато сразу понятно основное применение — оптимизация HashMap-ы когда множество ключей не влезает в память. Базы данных в духе ключ-значение... Хм. Как только на контестах появятся задачи на такие дела — сразу пригодится :D