rng_58's blog

AtCoder Grand Contest 009
By rng_58, history, 8 years ago, In English

AtCoder Grand Contest 009 will be held on Sunday (time). The writer is DEGwer.

Contest Link

Contest Announcement

The point values are 300 — 800 — 1100 — 1400 — 1600.

Note that the duration and the number of tasks is a bit unusual: 5 tasks in 2 hours.

Let's discuss problems after the contest.

  • Vote: I like it
  • +83
  • Vote: I do not like it

Comments Comments (24)
| Write comment?
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

So I can have a 4-hour rest for Venture Cup final, Tomorrow is challenging,

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Please make announcements a little earlier from next time.
EDIT: I didn't noticed that it is tomorrow.

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

sosad I thought end of the line is not needed... :'(

→ Reply
»
8 years ago, # |
  Vote: I like it +6 Vote: I do not like it

D is the same problem as POI Cave. That probably explains ko_osaga's 2 min AC.

→ Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Sadly, I solved problem D before :/

http://main.edu.pl/en/archive/oi/11/jas

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +6 Vote: I do not like it

D is a very well known problem from (old) POI. http://main.edu.pl/en/archive/oi/11/jas Sad that I realized that so late. In its original formulation it asks something like "minimal number of queries to perform a binary search on a tree".

Some people claim it is the hardest problem that has ever appeared on POI, I kinda agree with it.

EDIT: Heh, I see I was a litle late with telling this ;p.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    cave? Hardest problem on POI?

    reaally? xD

    Lanterns POI 16 or 17 finals says hi

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

What is wrong with my B?

I tried to fill depth[] using dfs, where depth[i] = sum for all it's children + 1 (it's the size of subtree rooted at i) Then I tried to greedily build the tree. Say we have a list of roots, at the beginning it contains only first node. On each iteration, while there are any unused nodes, we should add the biggest of possible nodes (for each root) and add it to roots. This solution gets WA.

I see that in editorial used some dp, but I can't realize what's wrong with this solution.

Link: http://pastebin.com/kRQngC2r

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can any one explain E? I have gone through the editorial, but did not quite get it. Looking at the codes, seems there should be some simpler explanation?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Reachable fractions are those whose k-ary representation is 0.a1, a2, ..., al, 0, 0, ... (with nonzero al) so that k - 1|M - S where S = a1 + ... + ak and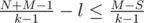 . Simple dp domputes that. I didn't prove it carefully, but after some thinking it should become clear why those conditions are good and not some others.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +26 Vote: I do not like it

    I also viewed the process as a rooted tree with N+M leaves, N of them labelled with 0 and the others labelled with 1, where each non-leaf node having exactly K children and is labelled with the average labels of its childeren (just like the editorial).

    Then I relax this condition a bit, so that there may be fewer than N+M leaves; I still require M of them to be labeled with 1, but between 1 and N of them to be labelled with 0. We can always reconstruct this into a valid tree (without changing the label of the root) by repeatedly expanding any leaf labelled with 0 (labelling all new leafs with 0) until there are N leafs labelled with 0.

    Next I proved that we can transform any tree which has more than one branching node at some level into a tree which has at most one branching node at each level and the deepest level has at least one leaf labelled 1. The second part can easily be achieved by contracting nodes where all childs are labelled zero into one node labelled 0. The first part can be done by noticing that if there is more than one branching node at a level, there are at least 2*K-1 leaves in one of the levels below that level. In this case at least K of them have the same value. We can rearrange these nodes so they all have the same parent. We then contract the K nodes into 1 node with the same label. This does not change the label of the root. If the node was labelled 1 we have to expand one of the deepest nodes labelled 1, so that the number of nodes labelled 1 stays the same. We can repeat this proces until each level has at most one branching node.

    Finally we can now uniquely define the shape of the tree only by its height. When we know the height we can calculate the number of leaves: it has to be at least M+1 and at most N+M. We then see that if we decide for each level how many leaf nodes at that level we label with 1 (making sure there are exactly M nodes labelled 1 in total) this defines the label of the root node and each way of assigning these values results in a different value for the root node. The number of ways for this can easily be calculated with a simple DP. We then take the sum over all valid heights and we are done.

    My code (20 mins after constest)

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you for your nice explanation. I was wondering why you ran the loop till: nzero+none below:

      REP(i,nzero+none) REP(j,k) if(i>=j) inc(F[h][i],F[h-1][i-j]);

      was it not enough to run till none?

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain problem C? I have read the editorial but not fully understand it:

  1. Is it common to define two DP states (DP_X, DP_Y)? I could never come up with such solution before reading editorial

  2. Why DP_X(i, j) only updates DP_X(i+1, j) for all j ? Shouldn't it also updates DP_X(i+2, j), DP(i+3, j)...as the given array is sorted, so S[i+3] — S[i] >= S[i+2] — S[i] >= S[i+1] — S[i] >= A?

  3. I don't understand the "clear" part, what does the editorial mean for it has O(Q) complexity?

Sorry if the question is so dumb but I feel that this problem is worth learning...

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    My solution to C:

    1. State is: (where, which). Here where = at what index I am, which = is "where" is X or Y [So 2*n states].
    2. Suppose we are at (i, X). Now find out, new_where such that value[new_where] is the largest value not exceeding (value[i] + A — 1) [you can find it out using binary search or lower_bound]. All the values in the range [i + 1, new_where] has to be assigned to Y. Is that possible?
    3. You can answer this feasibility question using a segment tree and calculating the minimum difference between the adjacent values in the range of [i + 1, new_where].
    4. If not possible, dp[i, X] = 0.
    5. If possible, dp[i, X] = dp[new_where, Y] (because you have to assign all i+1...new_where to set Y, and this one counts the valid ones)
    6. However, there is a special case. What if new_where = i? That means, there is no value[] which is to be forced to Y. So dp[i, X] = dp[i + 1, X] + dp[i + 1, Y] since value[i + 1] may be both in X or Y.
    → Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it +5 Vote: I do not like it

    1. Sure. A natural way to consider this problem is adding the elements one by one, and only the last element in each set matters. So the state is something like DP[last x][last y]. But one of these two elements must be the i-th element, so you can split it into two one-dimension arrays. The technique is called "rolling array", which is useful when the space is limited. (Actually I don't know if this term is common in English since I only see this in Chinese articles.) If you consider the original DP table as a matrix, this means you only keep the last row and the last column.

    2. Note that we add the elements one by one, so you don't use DP_X(i,j) to update DP_X(i+2,j) or something. This condition is included in (DP_X(i+1,j)->DP_X(i+2,j)) so we will use DP_X(i+1,j) to update DP_X(i+2,j). Always consider "what's the recursion formula" first before you write a dp solution unless you are extremely experienced.

    3. Whenever you "write" a value, store the position in a stack. When you need to clear the whole data structure, clearing these positions is enough since non-zero values only exist in those positions. After you clear one position you can remove that position from your stack since it contains zero now. So one "write" corresponds to at most one "clear", which means the running time only increases by a constant factor. More intuitively, you can consider it as "undo" operations.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Thanks, both senpai, very clear explanation.

      A note on point 1 that yes rolling array is common in english I think, though I first learnt it in chinese article as well :)

      My confusion was why there is a need of two rolling array at the same time, and you answer this question already, thanks so much :)

      → Reply