minimario's blog

Amazing LCS Problem
By minimario, 8 years ago, In English

Hi friends!

Recently one of my friends shared with me the following problem: Given 2 strings A and B of length n, for each substring (there are n(n - 1) / 2 of them) of A, find its longest common subsequence with B.

I heard it's solvable in O(N2) (which is amazing, since single LCS problem is O(N2)), but I'm not sure of the solution! It's a really short and amazing problem, but I couldn't come up with anything. If you guys could help, that would be great!

Thanks,

-minimario

Tags lcs, dp
  • Vote: I like it
  • +39
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it +22 Vote: I do not like it

happy birthday:

http://www.sciencedirect.com/science/article/pii/S0166218X07002727

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +10 Vote: I do not like it

I already knew that problem, but that is one of the most magic things I have ever seen :P.

EDIT: Since I was requested I will try to give some rough ieda of that solution, but I don't remember details and I don't have time to go into them.

We can imagine graph of transitions of standard LCS dp. Our states are points (i, j) of grid [0, |A|] x [0, |B|]. We have edges (i, j) -> (i+1, j) and (i, j) -> (i, j+1) with cost 1 and if A[i] == B[j] then we have an edge (i, j) -> (i+1, j+1) with cost 0 (if I remember correctly it is better to think about dp counting mismatches, not matches — this is of course same problem). Min number of mismatches is dp[|A|][|B|] which is also a shortest path in created graph from (0, 0) to (|A|, |B|). Similarly min number of mismatches between A[i..j] and B is shortest path from (i, 0) to (j + 1, |B|).

We will call an edge u->v important if dis(v) = dis(u) + cost(u->v), in other words, if it belongs to graph of shortest paths. Now we can imagine that with time we will shift our start of A and recalculate dp. If done naively this is of course a solution working in O(n3), so we should do something more clever. If state (i, j) has an edge ingoing from (i-1, j-1) it is always important. Key idea is that if it has not, then something like that should be true: "on some prefix of time edge (i-1, j)->(i,j) is important but then (i, j-1)->(i,j) becomes important forever" (surely, at least one of them has to be important). What we need to do is to perform dp on time when edge (i,j-1) becomes important. This is by far not a full description (and it is possible I messed some +-1's or we need to consider outgoing instead ingoing edges or anything), but I hope it should be helpful in proceeding further. Rules for that dp should be simple and what we really need to do (count (mis)matches, not some weird times) should also easily follow, I hope.

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it -96 Vote: I do not like it

You can find LCS of two arrays in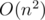 here (java implementation). Use same algorithm for strings :)

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks. How do I sort a string? Any help would be appreciated :)

    → Reply