Hello CodeForces)
I was solving one problem, and a lot of time I couldn't understand why i got WA
WA code ->
if (n > 1){
if (Check(n)) Update(n, 1);
else if ((ll)sqrt(n) * (ll)sqrt(n) == n) Update((ll)sqrt(n), 2);
}
AC code ->
double x = n;
x = sqrt(x);
if (n > 1){
if (Check(n)) Update(n, 1);
else if ((ll)x * (ll)x == n) Update((ll)x, 2);
}
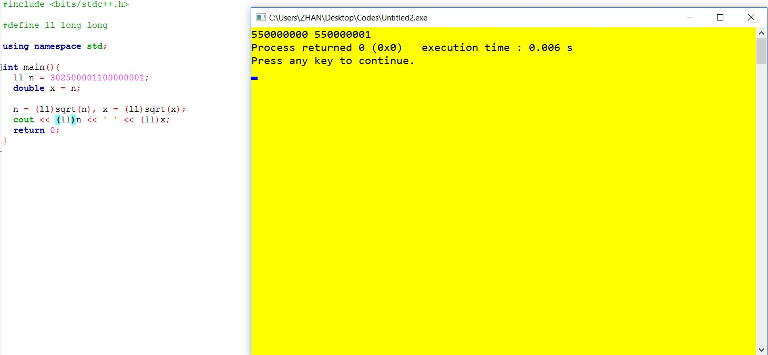
In first code if n = 302500001100000001 sqrt(n) = 550000000 but right is 550000001
I tryed to check in CodeForces custom test, it's error only in my and OJ compiler
Tell me why???
Give me some hint, how to upload photo in HQ???










tl;dr: precision, excess precision, and optimizer
Rule of thumb: do not assume that the result of floating-point operation is exact or repeatable, it's not always true.
See that example. Ignore all these
volatileand other hacks beforemain, they're required to stop optimizer's mess for demonstration purposes (see below).I believe the following happens:
doubleis typically a 64-bit double-precision IEEE 754 number, which has 1 bit for sign, 11 bits for exponent and 52 bits for mantissa.302500001100000001is100 0011 0010 1011 0010 0010 0101 1111 0110 0001 1110 1110 1011 0000 0001in binary, which is 59 bits length. Leading one is not stored for normalized numbers in IEEE 754, so only leading 53 bits can be stored, which results in trailing 6 bits (00 0001) to be rounded to00 0000because of not enough precision. That is, your number becomes302500001100000000when converted todouble, see the first line:x: 302500001100000000.000000000000However, GCC's
long doubleis typically a full 80-bit x86 extended precision floating point number. It has 64 bits for mantissa which is enough to store your number, see the second line:y: 302500001100000001.000000000000.sqrt's signature. It takesdoubleas the argument and returns anotherdouble. So, its input is always slightly less than you expected. However, it still prints "correct" answer:sqrt(x): 550000001.000000000000,sqrt(y): 550000001.000000000000. It's also correct when converted tolong long:to_ll(sqrt(x)): 550000001,to_ll(sqrt(y)): 550000001. Why is that?double. We're lucky here and its get rounded up, to the "correct" answer.long doubleas an argument and returnslong doubleas a result. We can see that roots are slightly different:sqrtl(x): 550000000.999999999069,sqrtl(y): 550000001.000000000000. I have not checked further, but I believe that the absolute difference is less thandouble's precision here.long long(which is basically "rounding to zero"), results become different:to_ll(sqrtl(x)): 550000000andto_ll(sqrtl(y)): 550000001.Frankly speaking, some sources claim that C++ should have an overload of
sqrtforlong doublewhich returnslong double. I believe it depends on the header used (<math.h>vs<cmath>) and compiler's version. In my compiler, there is no overload forlong doubleregardless of whether I use<math.h>or<cmath>.Ok, so now we see that if
doubleandsqrtare used, result is "correct" because rounding errors compensate for each other, in "incorrect" iflong doubleandsqrtlare used. However, your program does not seem to use any of the latter explicitly, so why does that happen anyway? The answer is, I believe, very typical:Believe it or not, operating with 80-bit floating point numbers is cheaper than with 64-bit, because the former are implemented in hardware. The latter are not. So, excess precision never hurt nobody, right? Right. Now let's perform all computations right in FPU registers without transferring values to/from memory where our short 64-bit double reside. That results in lack of rounding and more precise calculations. Actually, we have no control over which intermediate values are rounded (because there are not enough FPU registers and the value has to be stored in memory) and which are not.
And, finally, icing on the cake: there is an x86 assembly instruction
fsqrtwhich takes a square root and optimizer knows that it's whatsqrtis supposed to do. So, optimizer happily replaces call tosqrt(which would involve types conversion and stack frame allocation) with singlefsqrtinstruction. Voila — now we have ourdouble"replaced" withlong doubleandsqrt"replaced" withsqrtland we can start blaming excess precision.Why results differ from platform to platform?
I believe it's because the "bug" (which is actually not a bug) requires a lot of things to happen simultaneously. If either optimizations are fully turned off, or the optimizer does not have the insight about
sqrtof function, or its heuristics which decide in favor of doing everything inside FPU registers do not work well, bug is not there.What do we do?
My personal recipe:
epsto the number before converting or useroundfunction. Note thatepsshould be big enough to make some change: if you add 10 - 15 to 10000.25, it's not going to change anything, although 10 - 15 can be stored indouble. Also,epsshould be small enough to ensure that you don't "overround" your number.I'm sure no one read that till the end. Just upvote and think this guy knows well :P
imgur or something