rhezo's blog

How do I find the integer division of A/B under some modulo?
By rhezo, history, 8 years ago, In English

I need to do integer division, that is floor of A/B. Eg: 5/2 = 2.

Now consider the modulo to be prime, multiplying A with inverse of B and taking modulo is wrong.

What I said above is true because , 6 * inverseOf(2) = 3. But 5 * inverseOf(2) is not equal to 2.

So how can I do this?

  • Vote: I like it
  • +2
  • Vote: I do not like it

»
8 years ago, # |
← Rev. 2   Vote: I like it +37 Vote: I do not like it

If I understood correctly, what you want is to find some function f such that given A mod P = a , B mod P = b , then floor(A/B) = f(a,b) . This is obviously impossible. Consider this simple example:

Take P = 7. Since floor(11/3) = 3, then f(4,3) should be 3. But since floor(4/3) = 1, then f(4,3) should be 1 and we have a contradiction.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    No I meant that once we have a and b(as defined above), can we find A/B(integer division) as (a*inverse(b)) mod P? But I guess it can't be done.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      No, we cannot do that. Modular inverse has nothing to do with integer division, even though names sound similar.

      Another example: suppose P = 11, A = 13 (2 modulo P), B = 2. Then inverse(B) = 6 (because 2·6 = 12 = 1), but A·inverse(B) = 1, which is obviously not the answer expected.

      → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +21 Vote: I do not like it

What about using the fact that Integer division of A by B is same as (A — A % B) / B ? After this you can use modular inverses, either directly if prime or using extended euclid algorithm.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it -7 Vote: I do not like it

    Looks good, but for this I would have to maintain A%B too always. Since I wanted to do everything modulo some prime P initially, I would maintain everything modulo P only and it can get messy if B changes over many queries. For a single B, this would work I think.

    → Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

You may find A mod (B*n) = a, then A/B = a/B mod n

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How does this work exactly? And n is the initial prime modulo, right? (with which we need to find integer division of (A/B) ) ?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +8 Vote: I do not like it

      Yes. If A = Bnk + a, then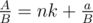

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Can you explain me please how to find (A mod (B * n))?

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it +10 Vote: I do not like it

          the same way you would do it with any other modulo?

          → Reply