Semifinal 1 will start in 43 minutes.
Broadcast: https://www.twitch.tv/topcoder_official
TCO Blog (I'm the blog writer): http://tco16.topcoder.com/blog/
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Semifinal 1 will start in 43 minutes.
Broadcast: https://www.twitch.tv/topcoder_official
TCO Blog (I'm the blog writer): http://tco16.topcoder.com/blog/
| Name |
|---|



Congratulations Petr bmerry and vepifanov with advanced to the final.
What's the idea for the 1000-pointer?
This problem has a few tricks. Firstly, if s = e return 0 immediately. Then, if s and e are not coprime, return 1. Now, suppose we let p and q be the smallest prime factor of s and e. (if either of them does not exist return - 1) If pq ≤ n, output 2, since we can go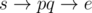 . Otherwise, there is no path of length 2. (otherwise suppose y ≤ n exist where s and y are not coprime, e and y are not coprime, but s and e are coprime. Then, y ≥ pq must hold since s and e are coprime and p and q are the smallest numbers which are not coprime to s and e respectively) Suppose 2p ≤ n and 2q ≤ n. Then,
. Otherwise, there is no path of length 2. (otherwise suppose y ≤ n exist where s and y are not coprime, e and y are not coprime, but s and e are coprime. Then, y ≥ pq must hold since s and e are coprime and p and q are the smallest numbers which are not coprime to s and e respectively) Suppose 2p ≤ n and 2q ≤ n. Then, 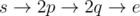 works. Otherwise, WLOG let n < 2p. This means that s < 2p so we must have s = p. However, the degree of p in the graph is 0, so there is no path from s to e. Thus, we return - 1.
works. Otherwise, WLOG let n < 2p. This means that s < 2p so we must have s = p. However, the degree of p in the graph is 0, so there is no path from s to e. Thus, we return - 1.
There are probably many ways to solve this. The intuitive idea is that we need to find a way to perform + 1 and × 2 operations, and the constraints hint that each operation should add 1 vertex to the graph. Let's ignore the weighted condition for now. × 2 part is easy, since we can add a new vertex v and connect 0 to v and v to 1, and no matter which side v is on, it will contribute 1 to the cut. For the + 1 part, the key is that we can add an edge from v to all future vertices, so for vertex v, if it's in the t-part of the cut, then it contributes to the size of the cut by 1. However, if it's in the s-part of the cut, the cut is a min cut only if all later vertices are in the s-part of the cut, or else the size of the cut will increase. (there are vertices from v to all later vertices) So, this step increases the size of the cut by 1, in the sense that there will be one more way to assign the vertices to the two cut sets, which is by assigning all later vertices (including v) into the s-part of the cut. So, it turns out that it is unneccesary to give weights to the edges.