egor.okhterov's blog

How to code this
By egor.okhterov, 8 years ago, In English

There was recently a problem called Sanatorium. It is relatevely easy and a lot of people solved it. I don't know why, but with some problems I experience difficulties which a normal human should not ever encounter :)

I have a picture in mind which I want to share with you and I'd like to see how would you transform it into the code. Please, do not use your own interpretations (though I'd be glad to see them) of the problem. Do not use your own representations. Just use the following picture: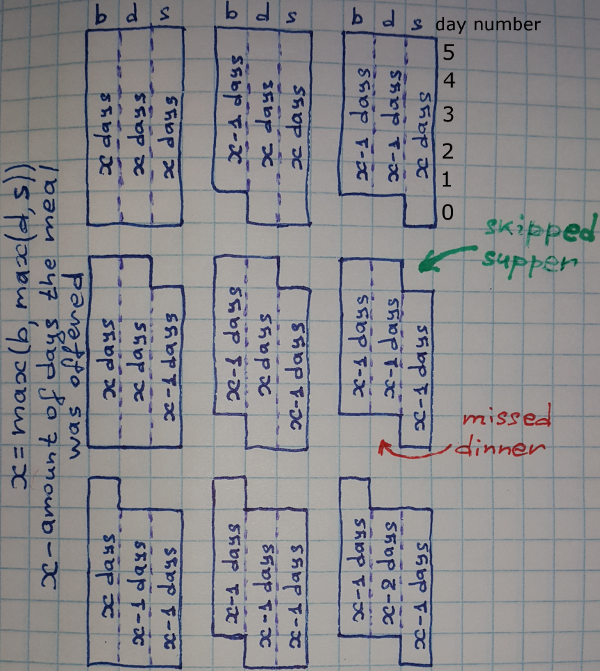

Each figure is a possible situation(state) for Vanya. We can enumerate all of the skewed rectangles with a pair of numbers (m, n). m — number of missed meals in day 0, n — number of skipped meals in day 5. The first rectangle is (0, 0), because we don't miss meals in the day 0 and we don't miss meals in day 5. Now the problem that I have is fitting (b, d, s) inside of these skewed rectangles. For example, if we are given (b = 6, d = 5, s = 5), we cannot use skewed rectangle (1, 0) (which located to the right of the very first rectangle), because it has x-1=5 breakfasts instead of required b = 6 meals in the morning. As I see it, the input (b = 6, d = 5, s = 5) splits all the possibilities (there are 9 of them) into 2 non-overlapping sets:
PossibleSet = {(0, 0), (0, 1), (0, 2)}
ImpossibleSet = {(1, 0), (2, 0), (1, 1), (2, 1), (1, 2), (2, 2)}

And we can check now the number of missed meals inside the PossibleSet: PossibleSet = {(6 - 6 + 6 - 5 + 6 - 5 = 2), (6 - 6 + 6 - 5 + 5 - 5 = 1), (6 - 6 + 5 - 5 + 5 - 5 = 0)}

So we can get the minimum number of missed meals 0 = min(2, 1, 0).

My brain refuses to produce the code out of these very thoughts.

Please, note that this is not the usual ask for help of how to solve the problem. This isn't merely about solving the problem. This one is about thinking process and it's correction.
I'd be glad to see the transformation steps (as detailed as possible). How does this picture smoothly translates into code (not just the final solution — there are plenty of those already). Maybe it will help me bridge some psycological gap that I currently have in my brain.

  • Vote: I like it
  • +22
  • Vote: I do not like it

»
8 years ago, # |
← Rev. 2   Vote: I like it +13 Vote: I do not like it

If you have 9 possible situations, good idea is to iterate over all of them and check each one. Each situation is described by the number of missed meals before an arrival and the number of skipped meals after a departure. So just iterate them:

for (int i = 0; i < 3; ++i) 
for (int j = 0; j < 3; ++j)

Next you should come up with checking of single situation. Here you can, for example, add 1 to each skipped meal (or subtract 1 from not skipped) and calculate amount of days as maximum value. During the contest, I coded exactly the idea, that you describe.

Also you made mistake: There is no ImpossibleSet because we can get each of the situations buy adding some values to b, d, s.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 4   Vote: I like it +1 Vote: I do not like it

    You are subtracting from b[k], but b[k] is the number of meals he has eaten. I don't understand how you can reduce the number of meals that he has actually consumed. In my view I would subtract from the meals that he was potentially offered. That is, we have maximum number of meals that he has eaten: int maxMeals = max(b, d, s). We have upper boundary on the number of each meals he has seen:
    int upperBoundForOfferedBreakfasts = maxMeals;
    int upperBoundForOfferedDinners = maxMeals;
    int upperBoundForOfferedSuppers = maxMeals;

    Probably, he has missed the first breakfast, that means instead of upperBoundForOfferedBreakfasts he has seen upperBoundForOfferedBreakfasts - 1 breakfasts. But if b is is equal to upperBoundForOfferedBreakfasts we cannot reduce that upper bound and that means he has actually seen all of upperBoundForOfferedBreakfasts.

    Am I wrong?

    → Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Let x = max(s, b, d)
If you look closely there are only three distinct configurations available , they are : {(x, x, x), (x, x, x - 1), (x, x - 1, x - 1)} . Now we need to find the minimum meals skipped so it's enough to bring their count to x - 1 if they are less than x - 1 . This is true because there is always a valid solution if we do this.

CODE
→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The last configuration is (x - 1, x - 2, x - 1). Isn't it?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Substitute y = x - 1 , in this case the max itself is y

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Why you can so easily make such substitution? Why not substitute y = x - 2?

        I can say what is the meaning of x and the meaning of x - 2. But what is y?

        For me it looks like the following example. We have x = 7 days in a week, 2 days are weekend (Saturday and Sunday). So we have x - 2 working days. I genuinely don't understand what you are substituting here.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          What I'm trying to say is that in the last case you are arriving before supper on day 0 and leaving after breakfast on day 6 . So here the max itself can be only x - 1 that is 5 here . This is what I meant by substitute y = x - 1

          → Reply