Let us discuss div2+div1 today's Opencup problems here
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 154 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/22/2025 10:59:33 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










How to solve div2 D Nice set of Points?
There was similar problem on Yandex finals 2011 (link). Solution on Russian is explained here.
How to solve B and J?
B — Let's say that 2 points are connected if they can be paired. it's possible to pair 2*N points iff each component of such graph has even size (I don't know proof). To make number of edges linear connect each point only with 2 closest points in each direction (not 1 point because this point can be deleted). Now we need to check if sizes of all components are even if we delete a vertex. This can found with similar approach to finding articulation vertices.
Code
The proof is obvious if you know Tutte theorem. Let's assume the graph is connected and |V| is even. If we delete vertex v, there will be at most 2 connected components(one will contain vertices on the same vertical as v, other will contain vertices on the same horizontal). Therefore, if we delete k vertices, there will be at most k + 1 connected components. If for some subset of size k after deleting it there will be k + 1 odd components, then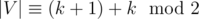 which is odd. Contradiction.
which is odd. Contradiction.
sorry, this not, the sol to the problem J
J — I have some shitty dp, but some team solved it very fast so I believe that there exists neater solution.
A simpler approach: DP[position in array][mask of used positions in permutation][remainder]; code.
Nice! On the other hand my solution is polynomial :)
Can you please explain the idea behind it?
Let's process positions one by one. We'll keep track of current position, mask of entries in the final permutations which we already picked and remainder of current distance. The trick is — in case you know that mask, you can calculate how many times you'll pass through the next segment (and therefore how much does it add to the total length of the route) — for each two adjacent positions in your route you can check the mask and see if they are on the same side of the segment or not.
Can you please explain your parameters?
Can you please explain your sol?
And G?
My code. It generates correct board for every prime k with size k2 × k2 and k3 zeros.
How to solve H?
The solution is based on Sprague–Grundy theory. Let's solve the problem where we have only one bean:
We are going to calculate the grundy function for each i. According to the theory:
Gi = mex(Gi - Ci, Gi - Ci + 1, ..., Gi - 1), where mex is the minimum non-negative integer, that doesn't appear in the set (e.x. mex(0, 1, 4) = 2 ).
To find it on O(logn) I used a segment-tree, where I kept for each number in range [0, 105] it's last appearance in G. Having this information, we run a simple recursion to find the minimum number, which last time appeared earlier, than i - Ci. It is our Gi, now we update the tree.
After calculating G, let's calculate the answer. According to the theory, Ggame is the xor-sum of all Gi, such that Ai is odd. The answer is "Second" if Ggame is equal to zero, otherwise "First".
code
How to solve E and F?
E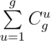 , where gcd(u, h) = gcd(g - u, w) = 1.
, where gcd(u, h) = gcd(g - u, w) = 1.
You need 3 facts (I'll list them without proof). First, our trajectory has period g = gcd(h, w). Second, if the trajectory period has u up moves (along h side) and r right moves, then gcd(u, h) = gcd(r, w) = 1. Third, any trajectory satisfying these constraints is good, so the answer is
F
Note that every empty cell that's neither start nor finish has exactly one vertical and one horizontal connection. This means that for every line (row or column) we can go from one side and greedily pair empty cells with connections (this implies the number of empty cells is even). This works for all lines that contain no end points and gives a hint where finish can be located: if there's 0 lines with odd number of empty cells, it is in the same line as start, if there are 2 — start must lie in one of them and finish in the other, and if it's more than 2 — the answer is NO. We have O(N) candidates for finish, we just check all of them and construct the path in O(N2) for each. I heard this solution can even be improved to O(N2) if we build DSU over the paths once for every line where we check the finish position.
Are Opencup problems open to the public?