We want to say thanks to Sereja for the translation.
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 154 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
We want to say thanks to Sereja for the translation.
| Name |
|---|



Div 2A :/
Can somebody explain me Div2C? Short code with explanation would be nice
First note that the binary representation can have 18 digits at most. That means we can have numbers from 0 to 2^18 — 1. Creating a 2^18 array is possible.
Now you must convert the given number to its binary representation. Then, if the operation is '+' you add 1 to v[number] or remove 1 from v[number] if it's '-'.
If the operation given is '?' you must get the decimal representation of the binary number given and simply print v[number].
My code: http://codeforces.me/contest/714/submission/20591279
Can someone please explain why this solution(20603277) giving TLE? Thanks.
Adding two string might have linear complexity — try to push back chars and at the end simply reverse string
If I reverse the string in after every step then it should take more time I think.
No, for example in function add you do s1 = "0" + s1; something near n times. Single + operation for strings might be linear, so n times s1 = "0" + s1; can cost you o(n^2).
If you simply push back char in time o(1) n times and then simply reverse string, the whole function will cost you o(n) (because you reverse once in linear time).
Not able to understand division 2 B solution,can anybody please explain why it is "NO" if there are 4 distinct integers?
I understand it but not at all, for this example:
n=2 : 1 4The answer don't should be 'NO'?" If there are two distinct numbers in the array — answer is «Yes» "
in this example you can take your x as 3
so 1+3 is 4
and we dont add anything in 4.
hence it is yes
Aaaa, ok. I understand the statement wrong. That x is a random one, I thought that x is from array.
Let your final number be Y .
That means initially the numbers were either Y , Y — X or Y + X .
Can't be more than 3 distinct integers .
Imagine there exists an answer Y, then we can only have 3 different int. i.e Y-x, Y+x and Y.
On problem Div1 C: Can someone give me a explanation of this passage? "We can just reduce number a[i] in array by value i and will receive previous problem.". I cannot understand why it is true :/
what does it mean "to receive the previous problem"?
It means the problem gets reduced to the previous one.
Why does it take 2LogN operations to find separating line in div1B?
We can find the smallest x, that get(1, 1, x, n) >= 1 and get(1, 1, x — 1, n) < 1 using binary search. To check if it valid we just need to check get(1, 1, x, n) == 1 and get(x + 1, 1, n, n) == 1. It takes LogN + 2. Overall 10LogN + 4.
I am not sure what is happening here in DIV 2C / DIV 1B / 713B....!!
Approach same as in the tutorial( 12log(N) ) + 4 extra query.
line cutting order right(x2)->left(x1)->up(y2)->down(y1)
but this approach got WA in test 55...!! WA_Submission
Then after seeing the testcase 55 i changed the order of the line
cutting to down(y1)->up(y2)->right(x2)->left(x1) and got AC...!!! AC_Submission
So are the test cases weak or am i missing something??!!
UPDT : My implementation of BS actually took 17 iterations instead of 16 giving max of 208 queries..!! :/
which caused me WA..!! :( bt now it seems to me judge data is weak given my
2nd approach with same BS implementation got AC...!! Again i think the problem had
too much tight constraints but failed to provide all possible tight corner case inputs...!!
Hope no one else faced the same situation..!! :/
+1s
Actually you can do only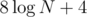 queries so the limits aren't tight.
queries so the limits aren't tight.
yes...realized that after the contest..!! :/
anyway solved it using 10logN+4
Hi ,
I apologize if my question seems stupid but I can not understand "For each i will bruteforce value j (i > j) and calculate answer for j if [i + 1, j] if arithmetics progression with step 1"
if i > j , shouldn't [ i + 1 , j ] be [ j , ... ] and expression if if isn't comprehensible ...
thanks in advance
Problem 1c can be solved in O(nlogn) without dp.
How to solve it without DP?thx
For simplicity, first subtract each number by their positions i, so we need to make the sequence non-decreasing.
Now, start from beginning. Each time a modification is needed, there are two options: raise the current position up or push elements before down. It should be noticed that for each position raising up happens at most one time (probably more than one unit though).
If nearest elements already form a equal sequence then all of them should be pushed down. However, pushing down n elements does not necessarily costs n -- some of them may be raised up before. For these elements pushing down actually contributes negative one per unit (for undoing raise). Furthermore, once some elements form a continuous equal sequence, they will be equal forever so we can view them as a group.
Now we are able to construct a solution. We start moving from position 2 all the way to the end. Once we move past a position some 'event' height will be recorded. There are three different situations:
1) a[i] = a[i-1]. In this case, position i simply merges with the previous group, and the cost of pushing down that group increases by 1.
2) a[i] > a[i-1]. We don't need to modify anything now; however an event point should be added at height a[i-1] for possible traceback afterwards -- when height is reduced back to a[i-1] two groups become one.
3) a[i] < a[i-1]. This is the only case we need an modification. Now, look for the cost for pushing down the previous group. As long as the cost does not exceed one (actually it never goes below one, you can prove it), it is worth doing.
i) If that is sufficient to lower a[i-1] to a[i], we are complete. Then the cost will increase by one.
ii) Otherwise, a[i] will be raised up. In this case, however, the cost will be reduced by one since when we push down position i afterwards, before it goes back to original value we are essentially undoing raise. Finally, we create an event point at original value of a[i]; when we reach that point later, cost of pushing down increases by 2 (from -1 to +1).
For implementation: store all event points in a heap(priority queue). When pushing down is performed, refer to the top(largest) value and update. Since each position adds at most one event point, total complexity is O(nlogn).
Tip: information considering the length, or left endpoint of a group need not be stored; what happens as we move past a event point is just that cost of pushing down increases. So the only thing recorded is: at this point how much does push-down cost increase? That is good for implementation since only a pair (height, costincrement) is needed.
You saved my day!
Can't it happen that you need to pop several elements from the heap? When you have e.g. 1,2,3,4,5,-100000 (you can lift it up to make positive).
Read last sentence again: heap.push happens at most n times. It is fine to have multiple pops at once, but by aggregate analysis it is O(nlogn).
I implemented quite similar solution, but using map, it seems simpler for me:
20623211 AC (time O(NlogN))
Works on random and sorted sequences of length 10^6 in 1 second.
For implementation, I want to share woqja125's AC code which is truly magical :D
Original code
Slightly polished code
Omg! Can you explain why does this work?
Amazing. Seems that there must be an much much easier explanation of this problem. Could you tell that magic idea?
See the comment below!
thanks a lot.
your solution is great and your explanation is very clear!
here is my implementation of the exact idea if it might help someone.
Will Codeforces ever stop posing questions with complexities of model solution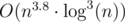 when there are obvious bruteforces in O(n4)?! Did any of testers even tried to compare those solutions? Did you try to ensure only intended solutions pass?
when there are obvious bruteforces in O(n4)?! Did any of testers even tried to compare those solutions? Did you try to ensure only intended solutions pass?
If the bruteforce solution is so obvious, why didn't you send it?
He assumed that organizers made sure naive solutions won't pass. It's about the constant factor, not about the difficulty of coming up with that solution.
1e9 in 5 seconds. I think it's obvious it will pass on CF, if you're on CF more than a year. I thought about it but I can't find a solution in that complexity, then I found the intended one. So maybe N^3 is not just a "obvious" solution? Intended one is really eaiser than that one except the implementation.
EDIT: Why "He assumed that organizers made sure naive solutions won't pass"? Organizers can make mistakes. Didn't you ever see a solution which have a more complexity than the intended one but with a simple code?
"1e9 in 5 seconds. I think it's obvious it will pass on CF, if you're on CF more than a year." — wut? You sure? You oversimplified it af. It heavily depends on kinds of operations you perform and number of them, locality of memory calls etc. I didn't inspect other people O(n3 + nt) solutions, but one I have in mind performs rather something like 1e10 operations with not very local memory calls, so it is obvious for me it won't pass. Btw people's times on this task are rather high, you can't really say it is obvious it will pass if one's time ends up being 4,5/5s :). As my saying goes "Problems can be divided to two kinds. One kind when intended solution for n<=1e6 and O(n log n) gets TLE and reason for that is "you know, big constant, memory allocation and shit" and second kind when for n<=1e3 intended solution is O(n^3) and organizers excuse is "you know, computers nowadays are really fast" :).
And regarding to "EDIT". If you take a look at constraints it is kinda obvious that test preparer's duty is to defend against >=O(n^3) or >=O(nt) solutions. These are not complexities taken out of nowhere, solutions in such complexities are not something crazy. I assume organizers are well aware of that and have taken care of that, tested few solutions with optimized memory locality and shit and ensured they don't pass.
"ensured they don't pass"
This part isn't about problemsetter. If you write smooth N^3 it will get an accepted if N<=1000. There's a lots of problem which is slower than intended one but pass like that.
I agree that it sometimes happens, but for this particular problem I do not consider O(nt) solution to be obvious.
That's why I don't like 2d problems. Always some naive stuff or in the toughest cases nsqrtn works better than any intended solution. And you can't really understand which nsqrtn solution is better (constants are rather unpredictable).
When I was solving this problem I easily got to the online max-queries. But I forgot about the existence of 2d-sparse table and understood that no log^2 (*log from binary search) tree would pass through time limit. I think I forgot about it because I can't really remember any problem which was solved with this algorithm, and I see the reason: some stupidity always works better.
P.s. n^3 + nt solution seems pretty obvious to me and it was the first thing I got to. Totally dislike the problem. And I still don't understand why this solution passes. 1.5*10^9 min(max()) + access to 2-d array operations in 3 seconds? Maybe tests are not good enough? I saw really not optimal solutions to pass in a half time and was surprised. Tests with 10^6 queries of (1000-eps)x(1000-eps) size should be good enough. I haven't checked if there are some so maybe I'm wrong.
Fun fact : it's harder than the author solution, but we can solve Div2C/Div1A using trie. Here is my code which i did during the contest: http://codeforces.me/contest/713/submission/20575096
lol, this is also the first solution I come in mind. All you should do is reverse the input and it becomes a standard trie problem :D
PS: do not forget to add trailing zeroes at the front to fill up required length
can someone explain why we can minus every a[i] by i without changing the answer ?
This might not be fully formal, but it's the way I thought about it:
A[i] < A[i + 1] can be written as A[i] <= A[i + 1] — 1.
Let's subtract i from both sides. ( Remember i is always >= 0)
We arrive at :
A[i] — i <= A[i + 1] — i — 1.
Which can then be re-written as :
A[i] — i <= A[i + 1] — ( i + 1)
We can also work our way backward, which proves the equivalence.
Now Assume the minimum cost for getting a non decreasing sequence for a[i] — i is x.
If you can make A[i] strictly increasing with changes less than x, then we could definitely make A[i] — i non decreasing using that value as they are equivalent, which contradicts our assumption that x is minimum.
As for the other way around ( x being smaller than needed ) you can use contradiction as well.
i think i got it :P thanks!!
Can someone explain the maxflow approach which was used by some participants for the Div2E/Div1C problem?
l1 ≤ r1, l2 ≤ r2. Am I the only one who have been stuck at this point?? According to the problem statement, 714A - Meeting of Old Friends, l2 cannot be smaller than l1 and same for r2. So 20579107 should get AC but it gives WA at 3rd test case. So correct me if I misunderstood something but problem statement is not corresponding to the editorial. That really effected me too much and caused me to get a great(!) motivation for other problems
I managed to get the idea of problem D but the TL seems really strict, my 2D sparse table got accepted with 49xxms out of 5000ms...
Your code can be a few times faster if you change
dp[N][N][11][11]intodp[11][11][N][N]. Ininit()you iterate over i and j jumping every 11 * 11 elements and missing cache very often.Please explain the DIV-2E/DIV-1C solution. I am not able to understand from the tutorial.
In the problem B.How can I read the answer after flush in c++?
simply using scanf or cin to get input from stdin
Problem 1E looks pretty similar to this.
I solved problem B differently. I used Binary Search to find the answer.
This is the source: http://codeforces.me/contest/714/submission/20612613
:O oppss!!! such a great solution!
mine- http://codeforces.me/contest/714/submission/20585222 :|
Overkill
Does anybody know a judge with this Div1C problem but with larger constraints (e.g. N = 105)?
There is a very short (10 lines!) and fast O(nlgn) solution for Div1C, proposed by woqja125 :
Start by subtracting i from all A[i]. We'll define fi(X) = Minimum operation to make A[1 .. i] monotonically increasing, while keeping A[i] <= X. it's easy to see that the recurrence is —
Observation : fi is an unimodal function, which have a nonpositive integer slopes. Denote Opt(i) as a point X which makes fi(X) minimum.
We will maintain those functions and calculate the minimum. we examine two cases :
Case 1 : Opt(i-1) <= A[i]. In this case, Opt(i) = A[i], and every point under A[i] have +1 slope.
Case 2 : Opt(i-1) > A[i]. This case is tricky. every point over A[i] have +1 slope, and every point under A[i] have -1 slope. Opt(i) is the point where slope of fi is changed into -1 -> 0. When observing the function, Fi(Opt(i)) = F(i-1)(Opt(i-1)) + Opt(i-1) — A[i]. We can simply assume that Fx(Opt(x)) = 0, and add this to our answer.
Since applying this operation doesn't contradict above observation, the correctness of this algorithm can be easily proved by induction.
To implement this, we can maintain a priority queue, which holds every point where slope changes by +1. It turns out that implementing this can be "extremely" easily done by O(nlgn).
implementation
Awesome! Thank you for your clear and helpful explanation.
can anyone explain the recurrence formulation again ? I am having a hard time understanding it ? what is Y ?
can you please explain the above algorithm in a more detail.Thanks in advance :)
We know f(opt(n)) is the final answer.
we only need to maintain f(opt(i)) for every i then we will get it.
we can find that :
when a[i] >= opt(i-1), f(opt(i)) will equal to f(opt(i-1))
when a[i] < opt(i-1), f(opt(i)) will equal to f(opt(i-1)) + opt(i-1) — a[i]
so if we know opt(i-1) when we add a[i], we can get f(opt(i)).
Let's consider how to maintain the information of fi to get opt(i)
In fact, we only need to know the slopes of every segment and then the point that slope become 0 will be the opt(i).
We save some "key points"(may overlap) in a sorted list, and the slope at position x is the number of "key points" that greater than x.
when a[i] >= opt(i-1), we only add a[i] to the sorted list
when a[i] < opt(i-1), we only need to move a rightest "key point"( which is equal opt(i-1) ) to the position a[i]. after that we add another a[i] to the list. You will find that we keep the property above to be unchanged.(because it means we add -1 to slope of (-oo,a[i]) and +1 to slope of (a[i],opt(i-1)] )
We only need a heap to maintain the sorted list.
Awesome solution. But can you please explain why do we have to push t two times when Q.top() > t? I'm having a hard time to understand that.
Because t is the point where slope differs by two (Ai - x to x - Ai). You will fail if you try to understand its implementation intuitively. I encourage you to fully understand above and implement it on your own.
Can you please tell how is it is evident that the recurrence function is uni-modal ? TIA.
Div1 E is very much related to this problem: Sequence
It will convert to this once you subtract i from each A[i]. After doing subtracting each A[i] you need to find minimum number of operations to make sequence non decreasing which is exactly what is asked in the other problem. As the tutorial for the problem I mentioned is relative simple any one can understand easily.
but that solution is O(n^2) and this is O(nlogn)
As far as this problem is concerned O(n^2) will pass. But always good to know better solutions.
dp[i][j] < 0 then dp[i][j] vertices to the right we still can visit...
I don't get what does this dp states mean, does it mean the interval [i+1,i-dp[i][j]] has been visited?
got it.
As it took me ages to figure out the recurrence for DIV1.C. I hope this will clarify things for others. Somebody already mentioned above that the problem can be reduced to a non-decreasing sequence by considering the sequence ai - i. From now on we will just consider ai = ai - i.
The second thing that one can prove is that there always exists an optimal solution, where one ai is not changed. Hint: Just consider an optimal solution where this does not hold.
Let bi be the sorted sequence of ai. Let dpi, j be the optimal value for the prefix a1... ai while ending in a value smaller or equal to bj. The recurrence is then as follows
dpi, j = min{ dpi, j - 1, dpi - 1, j + |bj - ai| }
Why? Either we let the prefix a1... ai end in a value smaller then bj - 1 ( hence also smaller then bj) or we let the prefix a1... ai - 1 end in a value smaller or equal to bj and also let ai be equal to bj. There are some base cases and this can of course be adapted for linear space.
Edit: 20669994
How do you prove that at least 1 ai is not changed?
If all numbers are changed, then we can increase (or decrease) all number by some amount until at least 1 ai stay the same
why we don't use another array instead using b ( sorted array of a) ???
Thanks mate this comment was super helpfull!!
I am having a very strange problem in QUESTION B — Filya and Homework
My submission is — CODE
When I run the code on my compiler, it works fine. However, it gives me a runtime error "on test case 1 itself!" when I submit it. I made sure I am using c++ 14 in both cases, so how can this happen?
Any help would be very greatly appreciated — stuck since a long time :(
Do NOT use return 1 in CodeForces, it will confuse the judge and thinks your code has RE.
Can someone prove why it is optimal to make all elements equal to the median ? (Sonya and Problem without Legend)
Because median is the element which minimize absolute sum of differences with all the other elements of the list.
Thanks .. But, I actually didn't understand what they meant by "make every element equal to the median of the prefix".
Did u understand this part : All the elements of the final array will be equal to some elements of the initial array?
God gives you everything