ibra's blog

Mirror of Bubble Cup Finals on Codeforces
By ibra, history, 8 years ago, translation, In English

Hi Codeforces!

We strike back from last year to held Bubble Cup again — programming competition organized by Microsoft Development Center Serbia for last nine years in a row. And this year's final is on this weekend!

Due to last year's successful experience we decided to organize a mirror of this final on Codeforces again. We would like to thank MikeMirzayanov and Codeforces for this great platform and their help. Competition will start at 11-th of September at 11 AM 12:00 (Moscow time). Contest will last for 5 hours and will go by ACM ICPC rules. It will be a competition for teams of 1-3 members. There will be 9 problems.

Contest was mainly prepared by employees of MDCS, knightL and Milanin. Additional thanks to bayleef and vitar for their help in testing.

This contest will be unrated (mostly because rules of this contest and not usual for Codeforces and it is still a mirror of onsite competition).

10 best teams will get T-shirts (each member get one), +10 T-shirts will be distributed randomly to competitors from top 100.

Please pay attention to that contest will start at 12:00 (by Moscow time)

  • Vote: I like it
  • +146
  • Vote: I do not like it

Comments Comments (62)
| Write comment?
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by ibra (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by ibra (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
  Vote: I like it -96 Vote: I do not like it

Inb4 >rated?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    ?

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it -72 Vote: I do not like it

      Greentext = quoting, inb4 = short for "in before"; full meaning: I expect someone to ask if it's rated because they're too lazy to read the whole blog post.

      UPD: Explaining when asked for an explanation = downvotes. Yep, just a normal day in CF comments.

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Will there be hacks? Will all submissions be tested by system tests during the contest?

→ Reply
»
8 years ago, # |
  Vote: I like it +30 Vote: I do not like it

Now, there is no option for teams :)

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Will there be live stats board?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    results of Buuble cup onsite will be revealed after the competition.

    → Reply
»
8 years ago, # |
  Vote: I like it +7 Vote: I do not like it

1 PC per team?

→ Reply
»
8 years ago, # |
  Vote: I like it +6 Vote: I do not like it

I thought that the mirror is going to be today. Now I have to wait until I can do a rage post about some amazing problems in the problemset... :(

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by ibra (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
  Vote: I like it +2 Vote: I do not like it

i hope i will enjoy . this is my first time :)

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

what is the difficulty of problems ?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Difficulty is that both divisions can participate. If you competed in last year's mirror, than i would say that difficulty is the same

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Is it a rated contest?

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +7 Vote: I do not like it

very hard problem set. matter of satisfaction that it is unrated.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yeah :D but as it is online mirror, so there is no way of being rated :D

    → Reply
»
8 years ago, # |
  Vote: I like it +8 Vote: I do not like it

How to solve the first problem?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    you have to reverse the given sequence at first. then multiply every term with non reverse one and at lust add all the product. thats the answer.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You just need to use magic numbers!

    20534967

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 3   Vote: I like it +8 Vote: I do not like it

      What do you mean by magic numbers?

      During the contest, we came up with a summation similar to the following:

      where Fi is the ith Fibonacci number. Is this correct? If yes, how to implement it? :/

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        It can be proved simply using recursion the answer is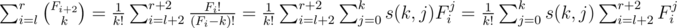 , where s(n, k) is the coefficient of xk in the expansion of x(x - 1)...(x - n + 1) (Stirling numbers of the first kind). We precalculate s(k, j) easily. Hence it suffices to to be able to find 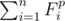for powers 0 ≤ p ≤ k. This can be done using Binet's formula + binomial theorem + geometric series sum. Use a struct to add, subtract, pow, inv, etc for 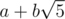for this purpose. I won't go through the tedious work, but the complexity I think works out to be O(k2).

        → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you please provide any link where I can learn about these numbers?

      → Reply
»
8 years ago, # |
  Vote: I like it +8 Vote: I do not like it

How to solve problem G ? :\

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 4   Vote: I like it +18 Vote: I do not like it

    You can transform the problem in to :

    Given some intervals, each interval cover some points and has a weight. Select a subset of the intervals such that the sum of weight is maximized and there isn't exist any point being covered more than x times.

    And this is a classic min cost flow problem.

    Node i represent position i in the crossword. Let the interval as from a to b with w weight.

    So you should calculate each interval. If crossword[i .. j] equals the word, add interval (i, j + 1, points of the word).

    First add edge with x capacity and 0 cost from source to node 0 and from node n to sink. Then add edge with infinite capacity and 0 cost from i to i + 1 for every i < n. Then for each interval add edge with 1 capacity and -w cost from a to b.

    The answer is the negative value of min cost flow from source to sink.

    This is correct because there is only x flow present. So it restricted each position will not be covered more than x times. And the flow tends to go to the negative edge, so it will give out the minimum value.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Why is it fast enough?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Something like 'Because it is about flows'. My MCMF with stupid Ford-Bellman got AC in 30 ms.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Our too. But it worked 0.5s on our maxtest.

          → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        It's O(n.Number_Of_Matches.x), As number of matches is <= nm, we have the total computations are at most 2.5e9 which is reasonable enough, considering how fast CF servers are these days.

        → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you very much , got it :D

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve problem D ?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 6   Vote: I like it +2 Vote: I do not like it

    To win the game, the xor of the pile sizes must not be zero. So we find the probability that xor of pile sizes is zero and subtract it from 1.

    Consider dp[i][j] which denotes the probability to get xor j for first i piles. The straightforward recurrence is:

    dp[i][j]=sum dp[i-1][j^k]*p[k] from k=0 to 100

    where ^ is the bitwise xor operator.

    But this is not good enough for the problem. We can do better. To calculate dp[i][j], divide i into two piles of size i/2. Then,

    dp[i][j^k]+=dp[i/2][j]*dp[i/2][k]

    Above is true when i is even. You need to modify it a little when i is odd.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you, got it

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Could you, please, elaborate a bit more. Why xor of pile sizes must be zero?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Sprague-Grundy theorem.

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Ok, understood.

          Now I have difficulties with the next thing below :)

          Could you explain how this thing works: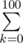
          dp[i][j] =  dp[i - 1][jk] * p[k]

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            a^a = 0 (xor operation)
            a^0 = a

            ((j^k)^k)=j

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              8 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              Wow, I feel very stupid now.
              I am sorry, but I still don't understand how this dp works :(

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                8 years ago, # ^ |
                  Vote: I like it +1 Vote: I do not like it

                First player lose if xor of N pile sizes equals to 0.

                So you want to know probability, that xor of i pile sizes equals to j

                (Answer will be 1 — dp[n][0]).

                This fact can be possible if

                • i-th pile have size 0 and xor of [i — 1] pile sizes equals to (j xor 0).
                • i-th pile have size 1 and xor of [i — 1] pile sizes equals to (j xor 1).
                • ...
                • i-th pile have size 1 and xor of [i — 1] pile sizes equals to (j xor x).

                Facts are independent, so total probability is simply sum of probabilities.

                → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +4 Vote: I do not like it

      I did the same, but then I thought we must multiply by n! because permutations will matter, so then I completely got confused about how to incorporate n! with fast expo.

      btw, its dp[i][j^k]+=dp[i/2][j]*dp[i/2][k]

      → Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

How to solve problem E ?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    As there is always a solution and the size of it doesn't matter,

    Do a normal DFS traversal , print each vertex you visit and change the color of it . Once you finish from a child print the current vertex again and change it's color because you will back to it , and if this child's color is pink then visit it again (without it's sub tree)

    you have to stop at node 1 or one of it's children , after visiting the last child of node 1 if color[1] is pink then back to it otherwise stop at this child .

    this code may help : 20538605

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve H?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please tell me why my same code for D get TLE and AC in different compilers? Thanks!

AC code: http://codeforces.me/contest/717/submission/20529231

TLE code: http://codeforces.me/contest/717/submission/20529203

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Your p[100] array is too short, iterating k up to 128 causes undefined behavior.

    The compiler does warn you about this. Use and read the warnings.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      Yes, the array is short when x=100. I never iterate upto 128 for this array. I don't understand why it got accepted in C++11 compiler when the array size is not sufficient. :P

      I fixed the size but it still doesn't help is eliminating the TLE on C++14 compiler.

      http://codeforces.me/contest/717/submission/20535200

      EDIT: Sorry, I see it now. Thanks for the help! :)

      → Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

I do like the problems~ so interesting! and it's really lucky to get into the top50~ thanks for the competition ^_^

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Problem H: Why does randomly dividing trainers into teams and then randomly dividing teams into two conferences work?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    wait for editorial, all explanations will be there

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    Because pretty much anything in this problem works so you can either spend hours to solve it properly, which in this case is a solution with guaranteed probability, ir just try to submit anything and get AC.

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Because the expected number of "crossing" edges in a random team and conference distribution is equal to .

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Doesn't the expectation depend on input i.e. wishlist of each trainer and hate pairs?

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone tell me how to solve G ? I know that is a min cost flow problem but I don't know how to build the network.

→ Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Check out this amazing solution that I discovered for problem D!

Complexity: O(XlogX)

It will be featured in the BC 2016 booklet, along with the proof.

→ Reply