The problem is this
After going through the submitted solution, I found the answer is this-> w! * b! * (w -1)* C(w + b — 3, n — 3)
Can someone please explain how this solution is coming.
Thanks!
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
| Название |
|---|



Lets split the final arrangement as ABC. A,C both have good events and B has not-so-good events. Now, within A,C the good events can occur in any order which is given by w! and within B, the not-so-good events can occur in any order which is given by b!
Now, assume we have only good events "GGGGGG" (some random arrangement) and the not-so-good events separately "BBBB" (again some random arrangement). We have to insert the not-so-good events somewhere in the good events such that we can get ABC. Since, we need atleast one event in each of A, B and C and we have w good events totally, we have (w - 1) positions to insert the bad events.
Till now we have w! * b! * (w - 1) which takes care of the different arrangements of the good and not-so-good events as described. The last thing we need to calculate is the number of ways we can split each of this arrangement into the given number of days.
It is clearly given in the question that each day, only one type of event can occur, therefore AB or BC cannot occur on the same day. So, we must have a split like this A|B|C. Total number of positions to insert a split is w + b - 1 (-1 because we cannot insert a split before the first event) and since we have already inserted 2 splits, total number of positions available now would be w + b - 3. Now, each split will increase the number of days by 1 and by inserting the 2 splits initially we have already got 3 days and so we need to make n - 3 days which means we need to insert n - 3 splits, which equates to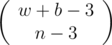
So, finally we get the answer as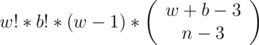
Hope it helps!
Can you please explain-> "since we have already inserted 2 splits"?
After we get a particular arrangement of the form ABC as described above where A,C have only good events and B has only not-so-good events, we need to separate the events into n days. But, we have an additional constraint saying that on each day only one type of event can occur. So, the last event in A and the first event in B must occur on different days. So, we have to insert a split between A and B. Similarly, the last event in B and first event in C must occur on different days, so we should also insert a split between B and C. So, we get A|B|C. Considering we have only this separation we have 3 days where A occurs on day 1, B occurs on day 2 and C occurs on day 3. Any further insertion of splits will increase the day by 1 and since we already have 3 days, we need to insert n - 3 more. Hope it is clear now.
Thanks