Решение этой задачи с помощью Heavy-Light декомпозиции очевидно. Но в обсуждении поминали какое-то решение за O(N * sqrt(N)) с помощью кластеризации. Можете кто-нибудь объяснить поподробнее?
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 152 |
| 6 | djm03178 | 152 |
| 6 | adamant | 152 |
| 9 | luogu_official | 149 |
| 10 | awoo | 147 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2025 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 21.02.2025 15:29:29 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










UPD2: Ниженаписанное не имеет отношения к тому, что спрашивал топикстартер. Зато объясняет эту задачу: 191C - Дураки и дороги
Не знаю насчёт кластеризации, могу рассказать другое решение за n log^2 n.
Разобьём каждый путь на две части части вершиной, являющейся LCA концов. Теперь пути идут только снизу вверх. Запишем в каждую вершину список путей, которые в ней начинаются и идут вверх. Теперь пройдёмся DFS'ом, помня для каждой вершины multiset глубин верхних концов путей, которые начались где-то ниже и ещё не закончились к текущему моменту. Тогда ответ для ребра, торчащего из текущей вершины есть мощность этого мультисета. Как его пересчитывать? Очевидно, что он есть просто объединение таких мультисетов для всех детей, из которого мы выкинули все пути заканчивающиеся ровно в нас. Как брать быстро объединение? Известный факт, что если примёрдживать меньший сет к большему за размер меньшего сета, то амортизированно выйдет n log n операций добавления в сет, что даст асимптотику n log^2 n. Очень популярная в прошлом-текущем сезоне идея, кстати.
UPD: интересно, что факт об амортизированной количестве добавлений log n на вершину доказывается как раз из соображений, похожих на использующиеся в heavy-light декомпозиции. По сути, такое решение соотносится с heavy-light-решением приблизительно как соотносятся для задачи на массиве подсчёт в оффлайне ответа на все запросы сразу с онлайн-решением деревом отрезков.
К слову, это решение сильно сложнее чем надо: так как сумма это обратимая операция, можно было просто дописать в нижний конец пути +1, в верхний — -1, и просто накапливать ответ. Но с каким-нибудь максимумом так не прошло бы.
Вы мне ИМХО объяснили C-шку со вчерашнего раунда...
И правда. Пардон, зато вышел интересный длинный комментарий не по теме :-)
Ну навскидку довольно просто можно за O(Q * (logN + K) + (Q / K) * (K + N * logN)), правда тоже без кластеризации. Если правильно выбрать K, то для макстеста будет порядка 128 миллионов операций. Идея следующая: будем для каждой вершины хранить максимум на 1, 2, 4, 8, ... предков выше. Если бы не было изменений, то ясно как отвечать на запрос за O(logN). Теперь применим принцип отложенной реализации, а именно: будем складывать запросы изменения в массив и затем применять их всех сразу, когда массив достигнет размера K. Получается, чтобы ответить на запрос, нам надо помимо поиска максимума в дереве за O(logN), еще пройти по всем запросам изменения, которые все еще не были применены и для тех, которые лежат на нашем пути, сравнить максимум с уже найденным. Получается, что отвечаем на один такой запрос мы за O(K + logN). Ну а перестраиваем все дерево с информацией о предках мы одним дфсом за O(K + NlogN), что происходит Q / K раз.
Я её решал таким образом в далёком 2007 году. Это как Heavy-Light декомпозиция, только я тогда не знал такой декомпозиции. Мы просто ограничиваем длину цепей до sqrt(N). Нам не нужно в таком случае юзать деревья отрезков для RMQ т.к. длина цепей ограничена корнем из N, мы можем запрос на изменение уровня радиации в цепи обрабатывать за O(длина цепи) пересчитывая каждый раз массив дающий значение максимума на префиксе. Количество цепей всего, может быть порядка O(N) (так же как для HL) но на пути между двумя вершинами будет не более двух корней. Для LCA юзаются цепи — у каждой вершины известны предок, и то к какой цепи она принадлежит, а каждая цепь знает самую высокую свою вершину "стартовую".
А как при таком способе построения цепей добиться того, что их количество на пути к корню от любой вершины будет маленьким?
Я решение писал давно, и мог ошибаться, но там юзается такой подход: каждый раз берём самую глубокую вершину из тех что еще не принадлежат никакой цепи, и вытягиваем вверх по предкам цепь, пока её длина не более sqrt(n) и вершины которые мы берём не принадлежат другой цепи.
Ну да, если брать самую глубокую, то вроде не тяжело доказывается.
Раз уж пошел небольшой оффтоп, поделюсь своим решением.
Сначала запустим dfs и для каждой вершины x запомним время входа в нее (s[x]) и время выхода (e[x]). Далее заметим, что если вершина y лежит в поддереве вершины x, то вершина z лежит на пути из x в y тогда и только тогда, когда s[x] <= s[z] <= s[y] и e[x] >= e[z] >= e[y]. Тогда максимум радиации на пути из x в y можно найти одним запросом к квадродереву, в котором каждой вершине x соответствует точка (s[x], e[x]). Ну и для нахождения ответа для двух произвольных вершин находим LCA и производим два запроса к дереву.
Может быть, не квадродерево, а двумерное дерево отрезков? А то первое вроде бы работает за линию. Извините, если ошибаюсь.
Не силен в структурах данных... Правильно понимаю, что двумерное дерево отрезков — если у нас дерево отрезков по первой координате + в для каждого значения первой координаты дерево отрезков по второй координате? Можно было и так решать, да (если сжать координаты), с учетом того, что у нас новые вершины не появляются. Я писал тупое разбиение прямоугольника на 4 части (это ведь квадродерево? :) ). За сколько оно работает — не знаю, как-то слышал странную оценку — O(sqrt(N)) на запрос, но на практике эта оценка у меня всегда подтверждалась.
Разбиение на четыре — это КД-дерево (см.ниже), и, да, оно работает за корень.
Квадродерево это вообще не в тему. Оно на плоскости а не на множестве точек. То что имелось ввиду это видимо KD-дерево. И оно действительно работает за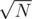 . И оценка абсолютно не странная. Каждый второй раз мы будем идти только в одну веток. Поэтому время
. И оценка абсолютно не странная. Каждый второй раз мы будем идти только в одну веток. Поэтому время  .
.
Да, это было KD-дерево. Спасибо, буду знать!
А как нужно его строить чтобы каждый второй раз идти только в одну из веток? как разбиваем множество на четыре прямоугольника? Нам ведь еще важно чтобы высота была относительно небольшой.
Казалось бы разбиваем на 2 вертиакальной ровно пополам. После этого разбиваем каждое множество на 2 горизонтальной ровно пополам и.т.д
Насколько я понял, имеется в виду обычное KD-дерево с поочередным разбиением по иксу и игреку. Вот мое доказательство трудоемкости в корень. Будем спускаться по дереву только в вершины, пересекающиеся с прямоугольником-запросом, но не содержащиеся в нем. Если прмоугольник-вершина не содержит ни одного угла прямоугольника-запроса, то за следующие два спуска мы в сумме никогда не спустимся более чем в два из четырех внуков. Значит, спуск в поддерево вершины без углов занимает O(sqrt(размер поддерева)). Вершин, содержащих хоть один угол запроса, на каждой глубине дерева не более 4, каждая из них в худшем случае заставит нас спускаться в одно лишнее поддерево размера не больше N*2^(-глубина), то есть общая трудоемкость O(4*(sqrt(N)+sqrt(N/2)+sqrt(N/4)+...))=O(sqrt(N)).
Разбиваем по иксу пополам. Это мы делаем xM = (xL + xR) / 2. или берём такой xM, что слева и справа одинаковое число точек попадает. и что делать если точка лежит на границе xM ?
Ну половину туда, половину туда. Ничего страшного там не будет. Если монотонно разбить, то совсем точно не будет.
http://pastebin.com/C9yxuGnb
Осторожно: исходник был написан давно и по-наркомански, например, хранит граф
Идея: представим дерево как дерево примерно sqrt(N) групп примерно sqrt(N) элементов каждая. Храним для каждой вершины ответ запроса до корня группы (считается, что корень группы либо корень дерева, либо сам принадлежит группе выше). Изменение — изменение в одной группе, она просто пересчитывается. Запрос (u,v) — поднимаемся от u, пока не дошли до предка v, и симметрично.
Примечание: нужно это делать очень аккуратно. Размер каждой группы может быть N, поэтому запрос на обновление вызывается только для потенциально изменившейся ее части. Гарантируется, что поддерево любого потомка корня группы внутри этой группы не превосходит sqrt(N)
Upd. madskillz-картинка.
Большое спасибо за объяснение. Именно про такое решение я и хотел услышать. Хотя, ИМХО, хеви-лайт идейно проще. Наверное, потому что я относительно свежий человек в СП (занимаюсь чуть больше года).
Реализационно то, что выше — халява, на самом деле. Никаких структур данных, ничего. Один DFS, который запоминает входы/выходы и возвращает число потомков, а как число потомков превышает заданную границу, ставит черную точку, пускает второй DFS для пометки ее группы, и возвращает 1.