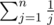shubhamgoyal__'s blog

Expectation Value Problem.
By shubhamgoyal__, history, 8 years ago, In English

Can somebody please help me out in this problem https://www.codechef.com/CDWR2014/problems/CW2/ My approach: Consider any number i.We can calculate its contribution in final sum.There are n-i numbers bigger than i.We choose any j of them and arrange them before i and rest (n-j-1) numbers are arranged after i. Thus the formula: 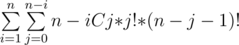This sum can then be divided by n!. I saw a few AC codes and somehow people have reduced it to sum of harmonic series,however Im not able to reduce my formula further. Can somebody please help!!.

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
8 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

This problem is same as LOOPEXP on spoj. Following is how I solved it but I am sure there are better approaches.

In this problem, we are required to find the number of times the min statement is true over all the permutations of [1..n]. Denote it by a(n). Suppose we know the answer for a(i) for i in 1 to n-1. Then we can write the following recurrence:

It can be derived this way. Consider where you put the "n" in a permutation of [1..n-1]. If you place it after the ith number, there are C(n-1, i) ways to select the first i numbers, (n-1-i)! ways to arrange the remaining numbers after n, a(i) executions of min over all permutations of the selected i numbers and i! execution of min because of n.

Now define b(n)=a(n)/n! (this is what we need) and observe the difference between b(n) and b(n-1). This should get you the required answer.

I hope this helps.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Thanks for your explanation. I was just wondering if you could help me reduce down my formula to sum of harmonic series.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 3   Vote: I like it +3 Vote: I do not like it

      Yes, it can be simplified to the correct answer. Sorry, I did not notice before that it is correct.

      Rewrite the term inside the sum as (n-i)!*(i-1)!*C(n-j-1, i-1).

      So we have to evaluate:

      Use hockey stick identity to prove the above. So we are left with:

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The second sum over j can be from 0 to n - 1:

→ Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it +3 Vote: I do not like it

I think this approach is easier.

Let Ij be the indicator random variable such that Ij = 1 if the jth element on a given permutation is less than all elements before it, and Ij = 0 otherwise.

We are interested in E(X) = E(I1 + ... + In) which by linearity of expectation is .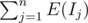

Then,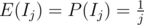 . Since if we consider a permutation of j elements, all of them are equally likely to be in any of the j positions. Hence, the probability that the jth element is the lowest is

Thus, the answer is

→ Reply