GlebsHP's blog

Codeforces Round #364 problem analysis
By GlebsHP, history, 8 years ago, In English

Finally, the analysis is here! Feel free to ask in comments for any unclear part.

Problems ideas and development:

Cards: MikeMirzayanov, fcspartakm

Cells Not Under Attack: GlebsHP, fcspartakm

They Are Everywhere: MikeMirzayanov, fcspartakm

As Fast As Possible: GlebsHP, fcspartakm

Connecting Universities: GlebsHP, fcspartakm, danilka.pro

Break Up: GlebsHP, MikeMirzayanov, kuviman

Huffman Coding on Segment: GlebsHP, Endagorion

Cool Slogans: GlebsHP

Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
  • Vote: I like it
  • +112
  • Vote: I do not like it

Comments Comments (56)
| Write comment?
»
8 years ago, # |
  Vote: I like it +24 Vote: I do not like it

The length of any simple path in the initial graph doesn't exceed n, so there are no more than n - 1 edges to delete and check.

F***, I'm stupid

→ Reply
»
8 years ago, # |
  Vote: I like it +11 Vote: I do not like it

A solution for 1B pairs node a[i] with a[i + k] where a[] is the list of nodes sorted according to dfs visit time. Can someone prove why this works?

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I applied the same logic as explained in editorial for Div2B but still get WA on testcase 31. Please help.

http://codeforces.me/contest/701/submission/19334389

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    row.size()*col.size()

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Sorry, if I am asking a lame question but what is wrong with that?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        set::size() returns size of a set whose type is size_t, which is unsigned int. So overflow on multiplication.

        → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it -26 Vote: I do not like it

why so late:(

→ Reply
»
8 years ago, # |
  Vote: I like it +35 Vote: I do not like it

I couldn't understand the analysis for problem E, so here is an explanation of my solution using a suffix array (19407933) for problem 700E - Cool Slogans:

Let's call a good substring either a single character, or a substring starting and ending with a smaller good substring, with no other occurence of that smaller substring in the middle. A maximal chain can be transformed into another maximal chain of good substrings, so we only need to consider those.

The repeated substring of a good substring is the previous good substring in the chain.

Actually, there are exacly n good substrings : for each position i, we can consider the largest good substring starting there. It can't appear right of it, or we would have a larger good substring starting at i, and if it appears left, it can be matched with the occurence at i to make a larger substring. It also means we can build a tree on good substrings (i.e. on string positions), with an edge from s1 to s2 if s1 is the repeated substring in s2. We are interested in the depth of that tree.

Let's build the tree incrementally. We process the string from right to left (in increasing size of suffixes). We want to be able to compute at each position the size of the good substring. Assume we are at position i, with parent j. We know that substring s starts at i and j and we want to compute the size of the smallest substring starting at i with two occurences of s, i.e. the substring with exactly two occurences of s. Let's assume for now that we can know the last time we saw s. Then we know the size of the good substring of i. We can use the suffix array to find all other positions starting with s, and set i as their potential parent (i will only end up as an ancestor).

So the only thing left is to compute the last time we saw a good substring. When we see a substring, we can propagate our position upwards in the tree (update all its ancestors with it). It is however too slow, as the tree can have depth O(n). We can transform this by setting a value in one node and doing subtree minimum queries. Subtree minimum queries can be solved using a segment tree on a static tree, but here building the tree and queries are interleaved. A solution could be to use an euler tour tree, but it is actually possible to use a segment tree in this case, as even though we don't know the shape of the tree in advance, each time we add a node, we know the size of its subtree (the number of substrings starting with its good substring), so we can give it a range in the segment tree with the same size.

Here is the main code with some comments:

Code
→ Reply
»
8 years ago, # |
  Vote: I like it +12 Vote: I do not like it

for div1B , i have no idea why my logic works , can someone give a proof/intuition. http://codeforces.me/contest/700/submission/19370545. I sort the 2K nodes according to dfs start time and pick nodes i , i + k.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +25 Vote: I do not like it

    Some informal proof: 1) Answer is sum of depth of universities (constant) — sum of LCA of chosen pairs, so to maximize an answer we have to minimize sum of LCA. 2) So we have to proof that sum of LCA is minimal when we pick pairs (i, i+k). 3) LCA of (i, i+x) never becomes more with x growing, so for every i we want to chose as big x as possible. 4) Now it easy to see that if we will never match some university from first k with some other from first k, because we will have that way some pair from second k too, and we can swap them with making LCA sum less of same easy way: ....1......1....k....2....2......=>....1..........2....k.....1.......2.... (1 and 2 are pairs number 1 and 2) , because x became more in both pairs. 5) So we just need to chose permutation of pairs of second k universities like: 123456 p(1)p(2)p(3)p(4)p(5)p(6) 6) Lets dist(i) = distance between pair number i. Now the main statement: dist(i)>=dist(i-1) in one of optimal solutions. Proof: let dist(i)<dist(i-1) for some i. Than we have next ....i-1 i....k...i(0 or more universities)i-1.... By swapping it to ....i-1 i....k...i-1(0 or more universities)i... we will never makes answer worse because if LCA of i-1 pair now became bigger by a than it's easy to see that LCA of i pair will become less at least for a (easy to see from that "new LCA's" of i-1 pair was definitely lost by pait i, and maybe even more because left i is righter and may have even depther LCA). 7) So dist(i)>=dist(i-1) and the only case when it works is when dist(1)==dist(2)==...==dist(k)==k because dist(1)>=k and sum of dists == k^2. All=) P.S. It's not informal now, but it was such in my head when I started writing))

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Could you please add contest tags?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

No idea what you are saying in 701D As Fast As Possible and 701E Connecting Universities... The description is really inaccurate. Can anyone explain the solutions in more details with better notations?

P.S: I know the formula solution to 701D. But I don't know how to use Binary Search in this problem.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 3   Vote: I like it +1 Vote: I do not like it

    In short you are building a check function with basic physics properties, and use binary search to choose the optimal time. (I will explain this with further details later... Gtg)

    UPD: Detailed explanation:

    701D- Code

    Key points of the check function:

    1. Everyone gets on the bus for the same amount of time, because we are trying to optimizing the time, so everyone should arrive the ending point at the SAME TIME.

    2. That means the bus is going to be going forward for (amount of each person's bus time share) * (groups of people) on the bus, and going backwards for (groups — 1) times to pick up the next group of students to get onto the bus.

    Here is how we calculate the variables:

    Each person's bus time share: (dist-v1*t)/(v2-v1), supposing that we are covering the distance which can't be covered by bare feet.

    Amounts of group: ceil(n/k), everyone is only getting on the bus for ONE time.

    The gap widen between the people on bus and who are not: (v2-v1) * (bus time)

    The time of the bus going backwards: (gap distance) / (v2+v1), we have to drive backwards to pickup the students who are not on the bus yet.

    Total bus time required: (bus time share) * (amounts of group) + (pickup time) * (amounts of group -1).

    The check result = (total bus time <= arrival time)

    UPD2:

    701E- Code

    All these observations are made under one assumption: The given graph is a tree- that means for two nodes there are only ONE(non-backward) path between them.

    I will take the editorial's example, assume that we have some nodes right here:

    A — B .... C — D

    Obviously for A we will try to get C or D, so does B... The question is: How do we determine if we are going to guarantee that there is such point C and D on the other side for A and B to connect?

    Here's an idea- we will try to find a point that has K universities on one side, and another K universities on the other side- In this way every link is going to pass through to point, and the total cost will be the total distance of all points from this central point.

    But don't be fooled! During a dfs search there are only children's — you can't determine if those children can be splitted into two sides. That's why we should be finding the point with the LEAST amount of child which has AT LEAST K children has a universities. In this way we can guarantee it is the central point we need.

    Now you should notice there is one thing left- Where is the root of the tree? Just pick any leaf of the tree and assume it is the root. That will do the job for searching the central point.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      In problem D there are still three things I don't understand

      Each person's bus time share: (dist-v1*t)/(v2-v1)

      The gap widen between the people on bus and who are not: (v2-v1) * (bus time)

      The time of the bus going backwards: (gap distance) / (v2+v1), we have to drive backwards to pickup the students who are not on the bus yet.

      Can you explain those?

      → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      "That's why we should be finding the point with the LEAST amount of child which has AT LEAST K children has a universities. In this way we can guarantee it is the central point we need."

      In my opinion, this is not obvious and should be proven, which I will do here.

      What your algorithm really does is find a point such that the sum of the number of universities in its children and itself is  ≥ k, yet that sum for any of its children is  < k.

      We find this point by starting with 1 which has the sum  = 2k > k.

      • If there is no child with sum  ≥ k, then we have found our point and stop.
      • Otherwise, in the case that there is a child with sum  ≥ k, then we go to one such child.

      We know that this process must end eventually, because otherwise, we'd be infinitely going down the tree which is impossible since there are a finite number of points. Therefore, we continue this process until we stop, at which point we have a child with sum  ≥ k, but with all its children  < k.

      Now, we make this child the root of the tree. What we want to prove is that we can create a pairing such that each pair goes through the root of the tree, which would obviously have maximum distance. This happens only when each pair has the lowest common ancestor of the root and we do this by mapping a university under one child to a university under another child.

      The new root has all of the children it had before, all of which had sum  < k, plus the fact that its parent from the tree is now a child, which must have sum  ≤ k because of how all of the other children combined have sum  ≥ k and there are only 2k universities. This means each child has  ≤ k universities under it. Now, each of the children of the root has a subset of universities and the root itself has a subset of at most one university, which creates an exact cover of all 2k universities where each university is covered by some child, but no university is under more than one child because that is impossible in rooted trees. Since each subset has  ≤ k universities, all of the others combined has  ≥ k universities (since there is a total of 2k), so there is an injection from the universities of each child to the set of universities from other children.

      Now, by proving that there is an injection from the universities each child to the set of vertices from other children, we have proven that we can map one university under any child to a university from another child without having repeats, meaning pairs can be made between universities of different children using all of the universities exactly once, which is exactly what we wanted, so we are done!

      → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Thanks man! Your explanation really clarified everything. :D

        → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      "Consider that the embarkation and disembarkation of passengers, as well as the reversal of the bus, take place immediately and this time can be neglected".

      The problem says that reversal of the bus doesn't matter. I AM CONFUSED

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        It means that it don't take time to turn the car around, or you could consider that the bus could drive backwards at the same speed.

        → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Awesome .....

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    The way they explained 701D with binary search was extremely convoluted, but hopefully, my binary search solution with comments will help you. The problem with their solution here is that their explanation is out of order, they never actually show their equation for what I called x, their variable posM convoluted their formula for x, and they never actually solve for what I called y but instead briefly mentions to account for the bus going back.

    However, I think the way they explained 701E pretty well other than the fact that lv is unnecessary since lv = 1 for all v. However, it is missing A LOT of detail if you're not so good at working with trees. Here's my commented implementation of the editorial solution.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      For 701D:

      Really nice explanatory comments! This shows the best way to understand a solution approach is to go through well commented codes implementing that approach.

      Can you explain as well how the direct formula is derived?

      On a side note, in your code, you could have used ceil() function to compute the number of groups. Is there any reason for not doing that?

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it +1 Vote: I do not like it

        The way I first derived the direct formula is kind of complicated (a linear system with numGroups number of variables and equations), but once we have the binary search solution like mine, this becomes more clear.

        See, for every group, we are adding x where

        Since x is constant for each group, we are basically adding numGroups*x to timePassed.

        For every group except the last group, we adding y where:

        Since $y$ is constant for every group, we are basically adding (numGroups-1)*y to timePassed.

        Thus, we have the following:

        timePassed = numGroups·x + (numGroups - 1)y

        Now, we can complete the journey in under mid seconds if and only if:

        timePassed ≤ mid

        Distribute out $totalDist-walkingSpeed \cdot mid$:

        Now, we have the following definition:

        Divide both sides by $c$:

        Add both sides by $walkingSpeed \cdot mid$:

        Divide both sides by \left(walkingSpeed+\frac{1}{c}\right):

        The left-hand side is the answer to our equation, giving us a very short solution.

        Also, yes, I could've used ceil() function to compute numGroups in my original solution. I could've also done (totalPupils+busSpace-1)/busSpace in order to keep integer division. However, I chose this way just because it's the way I first figured out how to do it before I knew that I could use ceil() to before I knew about the "adding denominator-1 to numerator" trick. It's just a habit.

        → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Why is eps 5e-7 ?

      → Reply
»
8 years ago, # |
  Vote: I like it +5 Vote: I do not like it

I don't quite get the part of optimizing the Huffman code implementation, can someone please explain it a bit more?

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For 701C, it seems that all the information are there, but have been put in such a haphazard way that it doesn't make much sense, or may be I am not that smart.

→ Reply
»
8 years ago, # |
  Vote: I like it -8 Vote: I do not like it

Too many mistakes, I can't understand a thing >_<

Does anybody have a clear explanation for problem D Div2?

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

In the analysis for 701E - Connecting Universities, I understood everything except for this statement.

"By the properties of the tree, paths from a to c and from b to d cover all edges of the paths from a to b and from c to d plus some extra edges, meaning the current answer is not optimal."

Could someone show me the intuition/proof for this property?

EDIT: I have proved it here

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it

    This is the first time I am explaining someone here on editorial comments. So if there are any issues please let me know.

    It is given that a,b both lie in the sub-tree of v whereas c,d lie outside it.Now just consider v as lca of a,b and u as lca of c,d. Also,let p(x,y) denotes the length of path from x to y. Then following equations will hold:

    (1) p(a,c)= p(a,v) + p(v,u) + p(u,c)
    (2) p(b,d)= p(b,v) + p(v,u) + p(u,d)

    Adding 1 and 2 will result into :

    p(a,c) + p(b,d) = (p(a,v)+p(b,v)) + (p(u,c)+p(u,d)) + 2*p(v,u)
    p(a,c) + p(b,d) = p(a,b) + p(c,d) + extra edges

    So considering a,b and c,d as connected universities is not an optimal solution. Now even if v is not lca still similar things will hold because that lca will lie inside the sub-tree of v and edges from that lca to v will fall inside the extra edges.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      There are several mistakes with this proof, unfortunately. Firstly, c maybe an ancestor of v. In which case you don't have to go all the way upto u and youre just adding a term. v may not be the lca of a and b. It makes more sense to consider, lca(a,c) and lca(b,d) separately both of which will be ancestors of v.

      I have written a proof. Will post it in a while.

      → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Let p(x,y) denote the length of the path between x and y.

    To prove: p(a,c) + p(b,d) > p(a,b) + p(c,d).

    Proof: Now, the LCA(a,b) is either a descendant of v or is v itself. [Since v is an ancestor to both a and b]

    Therefore, p(a,b) = p(a,LCA(a,b)) + p(b,LCA(a,b)) <= p(a,v) + p(v,b)

              p(a,c) = p(a,v) + p(v,c) [Since v is an ancestor of a, path from a to c must go through v]

              p(b,d) = p(b,v) + p(v,d) [Similarily]

              p(a,c) + p(b,d) = ( p(a,v) + p(b,v) )  + ( p(c,v) + p(v,d) )

               Here, the first term of R.H.S is >= p(a,b) as already shown. The second    term of R.H.S > p(c,d) since it is a path from c to d that doesn't go to LCA(c,d) first. Note that it is strictly greater since v is not an ancestor of c or d.

    Therefore p(a,c) + p(b,d) > p(a,b) + p(c,d).

    Hence proved.

    → Reply
»
8 years ago, # |
  Vote: I like it +21 Vote: I do not like it

Regarding to Huffman Coding on Segment. I think it is fine as an algorithmic problem, I enjoyed coming up with a solution. However I am not sure whether it was properly used as a task on a contest. After getting solution cleaned it is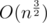 , however it is significantly harder both to code and to come up with than whole family of 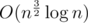solutions and given short amount of time on contest you should expect many solutions in that worse complexity. It is very dangerous complexity for n up to 1e5. Because of that getting this problem accepted boiled down to optimizing code in weird ways, playing with constants etc. Both of my friends who tried that problem on contest got their codes accepted only after that.

OK, so you can say "It sometimes happens that TL is strict and you need to optimize your code" or "If you try to get nonoptimal complexity accepted you are doing it at your own risk", but it is hard to create very good tests to that particular task, so I bet there are exist tests which cause many of ACed solutions to be few times slower, so there was no possible way of properly estimating whether particular solutions will get ACed. What is worse CF is not ICPC style, so even after passing pretest you don't have idea whether your solution will get AC and it can turn out it will if you would change magic constant from 300 too 400. Those particular tests caused that using transitions in Mo's in O(number of frequencies) on a light DS turned out to be faster than using set (according to Errichto. My well-written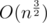 submission after contest took 2,7s (TL is 4s) whereas there are submissions taking 0,5s with worse complexities. You simply can't predict final behavior neither as a contestant nor as an organizer which made it a raffle whose solution will get AC and whose will get TLE.

Btw regarding to editorial it is not like "in order to avoid log in first part just use list". Neither of typical implementations of doubly-linked list allow you to insert element somewhere in the middle. Special adjustment to that task is needed which takes advantage of a fact that if we insert k then k-1 or k+1 was/is present just a moment ago/right now.

→ Reply
»
8 years ago, # |
  Vote: I like it +20 Vote: I do not like it

For the problem 700C — Break Up I compressed the graph into three separate MST's and did a similar algorithm to the editorial by considering only those edges. However, it runs in a faster complexity: O(N^2). Here is the submission if anybody is interested :P

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Could you explain it further ? Or just simply comment short explanation on your submission code. I've been recently curious about the problems !

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Hi... I wrote a piece of code for problem B. Cells Not Under Attack based on the problem analysis but I got WA on test 7. Can you help me to find out the reason, please? 19465299

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Interesting observation is that we are only interested in the longest word of each node of the suffix automaton of the given string (or the nodes of the suffix tree of the reversed string).

Can you elaborate this one? Solution is trivial with this statement but I don't get how to prove it...

→ Reply
»
8 years ago, # |
  Vote: I like it +25 Vote: I do not like it

700E - Cool Slogans can be solved without any suffix structures, just hashing.

My solution starts similar to Rafbill's — we can only consider only chains of good strings, where a good string is either one letter, or a string that has a shorter good string on the beginning and on the end, and nowhere else. Any optimal solution can be, going from the last string to the first, greedily transformed into this form.

We start with one-letter strings for all the letters in our word, this is level 0. If a word ends up on level i, that means we can construct a chain of i good words following this word. If we have a string s on level i, we consider all it's occurrences in the input — if we take any two neighbouring ones, we can make a word on level i+1.

If we just did this naively, then it would be too slow, because we would be "pushing" a single word with many occurrences through many levels (consider input "a" * n). However, if for a word on level i it's two neighbouring occurrences don't overlap, then it's good, because the word we add on level i+1 is twice as long. What if they overlap? Then we can see that this overlapping part is actually the word from level i-1. That means that those two occurrences of a word on level i must have been created by three occurrences of a word on level i-1. Going from the other side we can basically jump over useless operations — if on level i there are k consecutive occurrences of a string s, and all the k-1 substrings between them are equal, then we can already take all those k occurrences, and make a word on level i+k-1, instead of pushing this through all intermediate levels.

If we jump over levels as described, then we can see that we never get a string with two overlapping occurrences on any level, and thus each word will "go through" at most log n levels, because it's size doubles. So each position in the input will be considered as a starting position of some occurrence, of some string, on some level, at most log n times, which makes the solution O(nlogn).

The implementation is simple: for each level we keep a map from a hash of the word to all occurrences, and we sweep those levels in increasing order.

Code
→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Hi, I was trying to understand your solution and it turned out to be wrong. Here is a countertest: 13 abacababacaba The answer is 4(a -> aba -> abacaba -> abacababacaba), but you solution can't find 2 aba's in the middle and prints 3.

    → Reply
»
8 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

IN problem CONNECTING UNIVERSITIES I get an answer if I use long long int for all variables. If the limiit is 200,000, even int should do right? I get wrong answer on test case 11 if I use long int instead of long long int. Could someone please tell me how there is an overflow?

My code

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Consider the tree that is just a 200,000 length path (say the vertices in the path are in order 1,2,...,200,000) with a university on each vertex. Think about what the answer would be in this case (it would be too big to represent in a 32 bit int).

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

The problems are really nice in this round, so I hope someone will update the tutorial for problems C,D,E in Div.1.

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I cannot understand the tutorial of problem C http://codeforces.me/contest/701/problem/C please help me ,i spent too much time on it;

→ Reply
»
5 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

div1 B lv — length of the edge that leads from parent of v to vertex v; lv always = 1 ???

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In DIV1A/DIV2D As fast as possible,in second example 3 6 1 2 1,can't we achieve the result in 4.57967 seconds itself, if each of the pupil travels a distance of 2.84066 in the bus?

Like,first the bus picks up one pupil travels a distance of 2.84066,drops him,from there he walks,goes back picks up second pupil from position 1.42033(as he would have travelled some distance by now),and drop him after 2.84066,then go back and pickup last pupil from 2.84066(he would travelled this much by now) and drop him after 2.84066,and he walks from there.

Total time taken will be 4.57967

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Where is the tutorial for Problem F =((( I really need it

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

701-D As Fast As Possible : Here is the formula based approach for this question which i think is more intuitive and easy to understand. 1. We have to understand that all people have to reach destination at the same time (if not than the person which reaches earlier than others can be dropped from a bit earlier to save our time). 2. All the people will share equal bus time and walk time (as they have to reach at the same time described in point 1).

**SOLUTION :- **

group_num = (n + k - 1) / k , Tf = Bus forward time , Tb = Bus backward time pos = position of last group of people when bus arrives to them.

Now, As bus must have dropped (group — 1) groups before arriving to the last group so the time taken by bus is equals to (Tf + Tb) * (group — 1). So position of last group is v1 * (this time), i.e v1 * (Tf + Tb) * (group — 1).

and also this group will also travel for Tf time in the bus and will reach end point with all other. So, pos + v2 * Tf = l. And we know Tb = Tf(v2-v1) / (v2+v1) {can be easily proved}. putting values we get our Tf = l / { v1*(group-1) + v1*(v2-v1)/(v1+v2) + v2 } and Tb from relation.

And out ans will be group * Tf + (group-1) * Tb as bus moves group times forward and group-1 times backward.

here is my solution : 80667411

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why are the tutorials for Div 1. CDE not avaliable?

→ Reply
»
7 months ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

deleted

→ Reply