I was learning the topic FFT from e-maxx.ru (translated version). The english translation for this part "The discrete Fourier transform in a modular arithmetic" is not very clear on google chrome. Also, I am not able to understand clearly the math behind it. Please someone explain it.
Also, I have one doubt regarding the generators in number theoretic transforms. I was going through this solution of this problem. I understood the editorial and how to solve it using fft. But in the NTT solution (given in link) the author discusses about generators for certain prime numbers in comments. Can you please elaborate what are generators and how to calculate them?
Thanks in advance.
**EDIT: ** Understood the concept.











Why so many downvotes?
You cannot expect to understand NTT if FFT is not clear to you. If you want to learn about FFT, here's what helped me learn and understand it: http://web.cecs.pdx.edu/~maier/cs584/Lectures/lect07b-11-MG.pdf
Remember that you need the basic knowledge of complex roots of unity, or else the whole topic might seem a bit overwhelming. Good luck!
Hello, retrograd. I am able to understand FFT and how it works using divide and conquer (I read it from here ). I also have a basic understanding of complex roots of unity.
But I am not able to interpret the complex roots of unity in Modular Arithmetic terms.
An "n-th root of unity" is an element w which satisfies the equation wn = 1. For a fact we know that in the complex field, we have solutions of form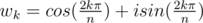 . You can use Moivre's formula to conclude that the roots are of form w10, w11, ..., w1n - 1. This is under the complex field, and it's what you should have been familiar with. However, there are other fields that have "n-th roots of unity", more or less similar to what we have discussed. For example, take Z7 and 2. We have that 23 = 1 in Z7, so 2 is a 3-rd root of unity. In fact, 20, 21, 22 are all 3-rd roots of unity in Z7. See the similarity here?
. You can use Moivre's formula to conclude that the roots are of form w10, w11, ..., w1n - 1. This is under the complex field, and it's what you should have been familiar with. However, there are other fields that have "n-th roots of unity", more or less similar to what we have discussed. For example, take Z7 and 2. We have that 23 = 1 in Z7, so 2 is a 3-rd root of unity. In fact, 20, 21, 22 are all 3-rd roots of unity in Z7. See the similarity here?
Thanks you retrograd, I understood your analogy. Please confirm whether I am right or not. In the example in e-maxx.ru site with P = 7340033, the author uses a generator of 5, and 5^(2^20) = 1 (mod P), meaning that with this generator, 5^0, 5^1.. etc. can be considered as complex root of unity in field of P. This also means we can cover a maximum of 2^20 values as well.
Thus, does it mean finding the generator depends both on modulo and N given? Please correct me if I am wrong.
You are correct :). There is an article that covers finding the generator, but I can't seem to find it. In essence, every finite field K incorporates a multiplicative group K * (the non-zero elements). In order to find the generator w, you have to find an element of order n in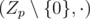 , which is a goup of order p - 1, so it automatically implies that n divides p - 1. If that happens, you can check elements' order sequentially, and one generator will pop out pretty fast (among the first 100 remainders or so).
, which is a goup of order p - 1, so it automatically implies that n divides p - 1. If that happens, you can check elements' order sequentially, and one generator will pop out pretty fast (among the first 100 remainders or so).
So isnt it like we have a general prime p=(2^k)*c+1
So we need to find a root of p of order 2^k.So first we find a root of order p-1 (lets say r and order x means r^x = 1 for firsttime for x ).And now we need to find root of order 2^k of p Can we say it is (r^c)???? .Lets say h
And ((h)^2) is root of order 2^(k-1) of p. So if we are doing ntt and we have a polynomial of size of 2^l. then we take root in first step as ((h)^(2^(k-l))
And for further steps should be exponentiation of it.
Am I right??
And now using a prime p=(2^k)*c+1. we can only multiply two polynomials whose size is less than 2^(k-1) What abt this??
sorry for really a bad question but why do we use modulo c*2^k+1 in FFT? Why don't use modulo 10^9+7 like in other questions? Also how is taking modulo 7340033 going to help us in having powers till 2^20 while we take modulo of coefficients of powers and coefficients can be anything(coefficients are not related to powers)?
We want to have root of unity such that w2k = 1. We can't find such value with 109 + 7 mod.
Why do we want root of unity such that w^(2^k) = 1? Can you share a resource which can help me understand NTT for competitive programming? I don't find any such explanation of this in e-maxx.ru site.
Because in D&C on each step we go from 2k roots to 2k - 1 roots. This is the very basics of FFT...
ok, i got what you are saying. But when do we use FFT with modulo instead of normal FFT?
When this modulo has 2k root of unity. Then every statement about usual FFT goes to the modulo FFT.
no, i mean why did we require to solve the question that is there in this post using modulo FFT when it can be solved using normal FFT(one without modulo)?
Some precision issues. If we want to have exact values when the inputs are integers we should better use NTT.
How does precision issues come? We only need to check if coefficient is zero or not zero. And when do we know that precision issues are more, so we should do it using NTT?
???
I mean in the question we only need to know whether that power has non zero coefficient or not. So how does precision issues come? And when do we know that precision issues are more, so we should do it using NTT?
You can also consider using NTT when in the question answer is required some modulo. For example, you figured out that the answer to the problem can be found out by checking whether the coefficients are zero or non-zero, but the solution is something like polynomial^k, where k is some large exponent. So here overflow issues may come in the coefficients of the polynomial, So NTT may be a better choice. Also sometimes, it is also required to find the coefficients of the polynomial some modulo. Thus NTT is the only choice instead of FFT.
Can you provide some materials for learning NTT ?
Try this. I used this to learn NTT.
I have written an Illustrated Guide for the Iterative Number Theoretic Transform Multiplication Algorithm.