Hello!
I am trying to solve this problem https://www.codechef.com/problems/QCHEF using Mo's Algorithm+Segment Tree but my solution times out. Complexity of my solution is 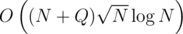 . Is it possible to eliminate the log factor? I know there is an editorial with the problem, (it uses a different decomposition, I think) but I am wondering if my solution can be optimised to
. Is it possible to eliminate the log factor? I know there is an editorial with the problem, (it uses a different decomposition, I think) but I am wondering if my solution can be optimised to 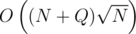 .
.
My solution: https://www.codechef.com/viewsolution/10638667
Thanks!











Seems to me like it can.
I didn't actually read your solution, but it most likely suffers from usual hard case in Mo's algo which is erasing some value from the interval when you need to change borders.
The first solution that came into my mind is with maintaining some structure like
deque <int> mp[MAX_A]and when you add some value X to the left yoump[X].push_front()andmp[x].push_back()if you add it to the right. To delete some value youpop_back()andpop_front()in a same way.Also you store
multiset <int>of values and after adding / deleting value you insert / erasemp[X].back() - mp[X].front()That's our bottleneck now, here's the log factor
To fix this log factor you should do it in a same way, you need to backtrack your changes instead of using set to keep them all.
There is a nice and short editorial with an example of code.