A bit less than five hours before the start of SRM 693 and no post by chrome — don't miss it! (No, I'm not the problemsetter :P)
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3846 |
| 2 | tourist | 3799 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3590 |
| 6 | Ormlis | 3533 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 9 | Um_nik | 3451 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 165 |
| 2 | -is-this-fft- | 161 |
| 3 | Qingyu | 160 |
| 4 | Dominater069 | 158 |
| 5 | atcoder_official | 157 |
| 6 | adamant | 154 |
| 7 | Um_nik | 151 |
| 8 | djm03178 | 150 |
| 9 | luogu_official | 149 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Mar/11/2025 08:10:15 (k3).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Am i seeing the right thing?
Getting a
MalformedURLException: unknown protocol: socketerror while trying to open the TopCoder Applet. How do I fix this to be able to enter the arena?Hmm, I'm not getting any error on this version of the applet.
Ah, same error on your version :(
Web Arena it is, then! Are plugins available for the web arena yet, any idea?
Then it has to be related to your system. It's definitely not purely server-side.
Enjoy your bugs.
Hard to learn about upcoming SRM's recently. No blog posts by chrome, no entry on clist.by or in Coder Calendar plugin :(
You can find them here: https://www.topcoder.com/community/events/
Somehow it is not on clist.by, maybe it is because we changed it into 'SRM' from 'SRM 693'?
It's very likely a parsing issue. You have a contest with the same name "SRM" later on July 9, and it may be overriding the current SRM on clist.by.
Yes, exactly.
It will always be now?
There was link like
http://community.topcoder.com/tc?module=MatchDetails&rd=...before. They go back?Is anyone successfully running the Java applet on a high dpi screen (on Windows 10, if it matters)? Everything is so tiny, and I can't seem to make Java recognize that it's not actually dpiAware :(
I tried to solve this problem for many years (note that MPSQAS also have this issue), but still can't find a good solution.
For Arena, one solution is to increase font size in Option->Editor, although it is not perfect.
How to solve the 250 pointer ?
DP. dp(i, j) denotes the max value of edges you can delete it you're at vertex i and j is the last vertex for which the edge (j, j+2) was deleted. If j==i-1, then you can delete neither (i, i+1) nor (i, i+2). Then you go to state dp(i+1, j). In the other case, you have a choice. Delete edge (i, i+1) and go to dp state (i+1, j) or delete edge (i, i+2) and go to state (i+1, i). Take max of both these values. The final answer is the sum of all edge weights — dp(1, -1).
A slightly different dp can also be done.
dp(i) = minimum sum of edges we can achieve by making nodes (i...n - 1) a biconnected component. You can use the fact that union of two biconnected components having a common vertex will also be a biconnected component.
The optimal solution should look like this: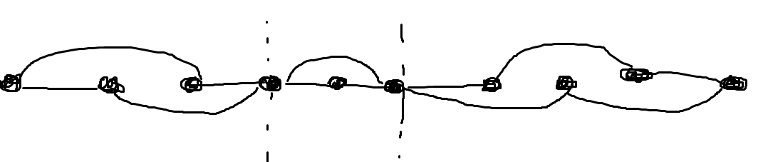
So it can be solved by a simple DP.
Are you the writer? Impressive Paint skills btw :p
Yes. Thanks :)
Thanks for the great problems!
Also, it can be solved finding max-flow min-cost in a graph with all edge-capacities equals to 1.
The max flow is 2. If in the optimal solution the resulting graph is not 2-connected then there exists a bridge edge and the max flow is less than 2.
I solved it using DP, was initially thinking of using maxflow-mincost but got stuck somewhere. Can you describe the exact graph?
The graph will simply be the given graph (with edges between i,i+1 and i,i+2) and costs w1[i] and w2[i].
How to solve 1000?
Repeat this: if there is a node with degree >= 3, mark this node red and remove it (and all edges linked to it).
So in the end, there will be no more than 20 red nodes and the remaining graph will be chains and cycles. Then we try 2^20 configurations for red nodes, do DP for remaining graph.
Ok, I'm not that good but I don't consider that DP easy anyway. Can you please explain some details? Basically, the chosen red points, for, let's say, a chain will just add restrictions like x and y: you can't choose both: x and y, and we want to know in how many ways we can choose some vertices, fulfilling these restrictions. But I don't think that this problem can be solve in polynomial time without relying again on the small number of edges from the initial graph...if we have to rely on that fact, how to do it? Sorry for my possible stupid question, but I really have no idea how to do the DP
After we fix a subset of red vertices, there are only three types of restrictions for non-red (say, black) vertices:
In order to avoid red-red-black triangles, you will get restrictions of the form "You can't choose black vertex x". In this case we can simply remove x from the graph.
In order to avoid red-black-black triangles, you will get restrictions of the form "You can't choose both black vertices x and y". Note that in this case x and y are always adjacent, so we can handle it using the property that the graph is chains and cycles.
In order to avoid black-black-black triangles, you will get restrictions of the form "You can't choose black vertices x and y and z at the same time". In this case the size of the connected component (in black graph) that contains x, y, and z is 3, so we can solve it by brute force.
Thanks! I understood. I didn't see that x and y should be adjacent.I don't know why I didn't think at this. Anyway, very nice solution, thanks for explaining, now is perfectly clear:)
For Div2 500, my solution was to remove edges greedily, in decreasing order of weight, and checking if the graph is biconnected. I couldn't code it up due to bugs, and I am not sure if greedy will work.
What was the correct solution?
Add all values from w1 and w2. Remove all positive edges for i=1 to n-1 (where n is size of w1) in w1. Don't know why this works. :-/
Oh, that makes the degree of each node equal to 2, so there are exactly 2 distinct path between any 2 nodes. Nice..
After removing an edge, a graph remains biconnected if there are 0 articulation points. If you observe carefully, we cannot remove any edges of w2 because then an articulation point will be formed. Now if we remove all but the first and last edges of w1, a cycle is formed which is biconnected. So we can remove all edges from w1 excluding the first and last. We shouldn't remove negative edges so that we minimize the sum.
Div2 Hard Solution: The resulting cycle is formed by several chains from the original trees, plus some new added edges. The weight of a new added edge can be moved to both endpoints. So now our problem becomes: use several chains to cover all the vertices exactly once so that sum of their weights is minimized. The weight of a chain a-b-c-d equals costV[a]-costE(a,b)-costE(b,c)-costE(c,d)+costV[d]. This can be solved by a classic treeDP.
Div1 Medium: (solution written by cgy4ever)
If there is no red edges and only blacks, then there are 0 perfect matches. When we add a red edge between node k and node A, the number of perfect matches will be increased by 3^k. So we can write n in base 3 and add such red edges. There will be at most 4*20 black edges and 2*20 red edges.
Multiple edges... are... allowed :'(
I didn't notice this initially as well, but then it seems that without parallel edges we can't get up to 1 billion matchings — K_{11,11} has less than 40 million matchings, but already more than 120 edges. That made me re-read the problem statement and notice the multiple edges :)
Could you describe your 250-problem solution?
Don't understand what is the meaning of best[i][0] and best[i][1] and why is it correct?