No problem was specially taken from "Wikipedia". For me it's really hard to understand, that problem "B" was there.
A (Div 2). (Idea : Gerald, realization : Aksenov239, code : 1670635)
If the lengths of 2 strings aren't equal — that means "NO". We try to find the positions in strings, where chars are different. If there 1 or more than 2 such positions — "NO". After that we swap 2 characters in the first string, and check for their equality.
B (Div 2). (Idea : Aksenov239, realization : Aksenov239, code : 1670637)
- We can see, that we can do all in integers, because k is integer number of percent.
- For each dwarf we should find his optimal strategy — to check 2 strategies with speed.
- We should sort them.
A (Div 1). (Idea : Aksenov239, realization : Aksenov239, code : 1652592) Let's propose, that after the i-th year, there is x triangles up and y triangles down. After another iteration we can see, that amount of triangles became — 3x + y up and x + 3y down. Let's see the difference between them: at the i-th it's x - y and at the i + 1-th — it's (3x + y) - (x + 3y) = 2 * (x - y). We can see, that difference between amount of triangles grown up by 2. Because on the i-th year the difference became 2i and all amount of triangles is 4i. We can see, that on the i-th year the number of our triangles is 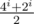 . That can be computed by modulo p using the fast-power algorithm.
. That can be computed by modulo p using the fast-power algorithm.
B (Div 1). (Idea : Aksenov239, realization : Aksenov239, code : 1652597) This problem was made by my love to inequalities. :-)! The answer for this problem is 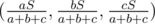 .
.
Prove: 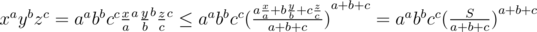 . (This is AM-GM inequality. Link for whom don't know it.)
. (This is AM-GM inequality. Link for whom don't know it.)
The equality becomes only, when 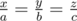 .
.
And you should check on zeroes. If a = b = c = 0 — you can choose any good answer — x + y + z ≤ S.
C (Div 1). No comments. :-)!
D (Div 1). (Idea : Aksenov239, realization : cerealguy, Gerald, Aksenov239, code : 1652604)
This is number theory problem.
I'm trying to explain it step by step:
1) Let's prove, that LCD is maximum 2.
Let  . Squaring both sides we get
. Squaring both sides we get 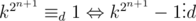 , but we want to
, but we want to 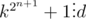 . This means, that d can be only 2.
. This means, that d can be only 2.
2) Let's make this lenghty product simplier.
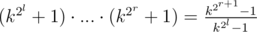 .
.
We can count this by modulo p fast, and divide it by 2r - l, if k is odd.
3) There is many interesting things in this solution.
Firstly, it doesn't work, when p = 2 — but it can easily done by you.
The other problem is harder, what if  , this means that for each i ≥ l :
, this means that for each i ≥ l :  , and this mean,
, and this mean,
that for each i ≥ l : k2i + 1 ≡ p2. And the product by modulo p is equal to 2r - l + 1.
E (Div. 1) (Idea : Aksenov239, relization : cerealguy, code : 1652611)
This problem wasn't taken to ROI, because of that I gave it here. This is pretty hard problem. I can't now realize, what cerealguy wrote, but his solution is O(nlogn) — without binary search. For me it's quite hard to understand, because my first solution was with binary search. And there were solutions, that has a worse asymptothic, but they run faster.
Because of that I can only give you key ideas, that can help you. (afterwards you can see the code of cerealguy)
Ideas:
- Let's find for each person the nearest subway point for them. It can be done in nlogn with use of segment tree or something else.
- We can see, that if one person goes to subway, the others, which distance to subway is smaller, can go to subway too — it doesn't affect the answer. Because of that we sort all persons by their distanse to subway.
- The area of the person, where he can come in t seconds, is romb. And we can intersect all rombes in O(n) — the intersection is like rectangle.
- Let's make the first intersection. When nobody goes to subway. We get a rectangle.
- The main idea, that for this rectangle — the nearest subway becomes always the same. We go throught people in sorted order, we can fast recalculate this small rectangle — and because of that we can fast recalculate the answer.
And we get a solution in O(nlogn) time. Ta-dams.
Thank you all for your attention. I'm deeply sorry about the problem "C".










For some time links for solutions isn't working. Temporarily:
А div. 2 — http://pastie.org/3884140
B div. 2 — http://pastie.org/3884143
A div. 1 — http://pastie.org/3884145
B div. 1 — http://pastie.org/3884147
D div. 1 — http://pastie.org/3884149
E div. 1 — http://pastie.org/3884152
great tutoriAL!!!!!!!!!!
I just think cf need to save the draft as I accidently click on some link and the content is lost……
I may need to borrow a book about number theory……
and at last……I just can't understand the product in C(Div.1)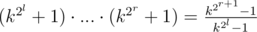
a rookie
Try this:
Multiply LHS by "k^(2^l) — 1" and get: (k^(2^l) — 1) (k^(2^l) + 1) ... (k^(2^r) +1)
Repeatedly apply the identity: (a — b)(a + b) = a^2 — b^2 (for every first two terms)
A (Div 1) : simple explain
suppose : up -> num of upward triangle and down -> num of downward triangle
Initially :
conculsion : each n we split each triangle to 4 triangles it's mean at n we have 4^n triangle we want to want how many of 4^n are upward
suppose : a -> num of upward triangle b -> num of downward triangle
fact :
conculsion :
also we see that sum of a' + b' = [ (2^n)+1 ] + [ (2^n)-1 ] ,
from (2) : a' = [ (2^n)+1 ] , b' = [ (2^n)-1 ]
[ a' + b' ] * c = 4^n
[ 2^(n+1) ] * c = 4^n
I solved Div1 B using Lagrange's Multiplier .
L(x,y,z,lamda)=x^a*y^b*z^c-lamda*(x+y+z-s) and then partially differentiating w.r.t x,y,z and equating to 0 gives x=a*s/(a+b+c) y=b*s/(a+b+c) z=c*s/(a+b+c)