→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3898 |
| 2 | tourist | 3840 |
| 3 | orzdevinwang | 3706 |
| 4 | ksun48 | 3691 |
| 5 | jqdai0815 | 3682 |
| 6 | ecnerwala | 3525 |
| 7 | gamegame | 3477 |
| 8 | Benq | 3468 |
| 9 | Ormlis | 3381 |
| 10 | maroonrk | 3379 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | Dominater069 | 161 |
| 4 | Um_nik | 159 |
| 4 | atcoder_official | 159 |
| 6 | djm03178 | 157 |
| 7 | adamant | 153 |
| 8 | luogu_official | 150 |
| 9 | awoo | 149 |
| 10 | TheScrasse | 146 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/31/2025 10:51:09 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











I get "sandbox returned nonzero (137):" on my old submissions. What does this mean?
Login timeout repeteadly on topcoder web arena. Anyone else facing the same problem ?
yeah, neither web arena works nor the applet.
What is the idea for div1 500?
Assume we can build a relation with exactly X invariant subsets on first N elements (call it (N, X) pair). If so, we can build the (N+1, X+1) pair (here N = 4):
... and (N+1, 2X+1) pair:
Now you should run a simple DP which shows you which (N, X) pairs are reachable (starting with (0, 0)). It turns out that N=17 is sufficient.
Thanks! Nice solution! But still confused about this, how do you guys come up with the idea that building the good set incrementally to exactly: x + 1 and 2x + 1, is there some intuition or have you just done similar problems before?
For me, it was just intuition. I tried several constructions which didn't succeed. Then I decided to build a solution incrementally. So, if I can do X on N elements, how can I use the next one? I can deeply tie it with other elements (almost not increasing number of subsets) or I can make it almost independent of others (doubling the number of subsets). I ran a simple python script to check if each number is reachable this way, and it turned out to be a solution.
Actually, if you consider an empty subset, like many participants did, it is a quite standard idea of representing X in binary and juggling with bit representation. I think most contestants came up with the idea that way.
After representing X in binary I ended up with an uglier construction. Let's say P is highest bit of X. We'll take a set of P elements with f[a][b]=b, so each subset of this set is good. Also we'll add 1 "bad" element, such that f[i][bad]=i+1, f[bad][bad]=0, so taking bad element forces us to take all set. This set will discard missed empty subset — right now we have exactly 2^P good subsets.
Now for each next '1' at position i in binary representation of X, we'll add one more element which will give us 2^i good subsets. In order to achieve this, we'll say that f[j][new_element]=new_element for j<i (so we can take any subset of first i elements plus our new element), and f[j][new_element]=bad_element otherwise (so if we'll take some other element — we'll be forced to take whole set, and such subset has been counted already).
Thanks, brilliant!
First, I'd say take the empty subset into account for convenience (
x -> x+1).Now, if we have a solution with
nitems andssubsets, we can do two steps:Make a solution with
n+1items ands+1subsets. For example, if0...n-1are old elements andnis the new element, maken$0=1,n$1=2, ...,n$(n-1)=0. Andn$n=0. This way, whenever we take the new element into our set, we have to take all old elements as well.Make a solution with
n+1items ands*2subsets. For example, if0...n-1are old elements andnis the new element, just maken$i=nfor everyi. This way, every old setScan now be duplicated asS+{n}.Initially, we have
0items and1subset (empty set). All that's left now is to constructxfrom1using operations+1and*2. Clearly, if we consider the binary representation ofx, we won't have more than10of each operation, sonwill be no more than20.Assume that the empty set is a good subset (so we are looking for a set with x+1 good subsets)
If you are given a set with n elements and x good subsets, can you construct a set with n + 1 elements and 2x good subsets?
If you are given a set with n elements and x good subsets, can you construct a set with n + 1 elements and x + 1 good subsets?
EDIT: Codeforces was slow when I posted this so it came out completely garbled. Just read Gassa's comment above.
Suppose we have table of size n and answer x.
Let's build table of size n + 1 and answer 2x + 1: f(p, n) = f(n, p) = p. It is easy to see that we can add element n to any good set and it remains good, and we have new good set {n}.
Let's build table of size n + 1 and answer x + 1:
Unable to parse markup [type=CF_TEX]
. It is easy to see that the only good set with element n is set {0, 1, ..., n}.Now we can solve the problem recursively: - x = 0 — empty table -
Unable to parse markup [type=CF_TEX]
— solve for (x - 1) / 2 -Unable to parse markup [type=CF_TEX]
— solve for x - 1The size of the resulting table will be no more than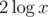 .
.
duplicate, CF sends my comment twice
Is there any test case that everybody have missed or there is some error with the judge? As everyone failed div2 250.
Some bug in the system tests, there was a notification about it.
OMG, I've just realized that in the "Batch test" output one should look not on the "Success: true" line, but on the "Correct example: false" :( I've just screwed up my 500 because of that...
LOL happened with me once, didn't happen again ever.
Oh, tell me how to use it! I use KawigiEdit, but today I couldn't easily test any problem at all. I once tried wrong solution at batch test and thought it just didn't work.
You save your solution, compile it and press "batch test". After that you carefully check that each test is passed by looking on "correct example" line (but not on "success" line!)
Could anyone explain their solution for Div2 1000 ? Thanks.
I solved this problem using dp and bitmasking. My DP table had two states, one for mask and other for the alphabet last placed. I stored the count of "available" alphabets in temp array. Dont count those for which mask is 1 as they have already been used. Now loop over alphabets for which temp[alphabet] is positive. Find any position i in first string which matches current alphabet and make sure that alphabet in forbid string at index i is not equal to alphabet which is being considered in the loop. Also check that alphabet last placed ( it was passed in recursion and is 2nd state of dp) is not equal to the alphabet you are considering now. If all conditions are satisfied proceed further with recursion. Here is the code code
Hey can you look at my soln. i used the same approach but i am getting TLE on large inputs :http://ideone.com/443DkL
How to solve div1 1000?
I tried 10000 times randomly rotate, then sort, then connect consecutive from left to right, and choose the best option — but it fails.
Could anyone explain the solution for Div2 1000 ? Thanks in advance.
See my post above.
How to Solve Div2 1000 ? Thanks in advance ...
Div1 should go like this. Firstly from wolframalpha learn that 0.636 ~= 2/pi. Then note that 2/pi is expected absolute value of sine function, so if we pick a random line (angle chosen uniformly) expected value of summed length of given matching's projections to that line is 2/pi of its original length. We need to find that line (random should be ok I guess) and produce nonintersecting matching of length at least summed length of those projections. We may divide those points to left and right part as their projections are ordered on that line and find any nonintersecting matching between those parts. Nonintersecting bipartite matching on a plane can be done by for example hungarian (we use minimum cost matching to find matching of sufficiently high length — ironic, isn't it :)?), but there are also many other ways.
Beatiful problem :).
Actually, we don't need to take that line from random solution. We do not need to find it at all. We just need to produce all possible divisions to two halves. Moreover only such halves that can be separated by line. There are n such divisions and we know that one which will be also determined from that good line will produce sufficient solution. That solution do not even need initial matching, it produces matching of length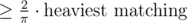
According to http://www.tau.ac.il/~nogaa/PDFS/noncros.pdf (which I've used during the contest :)), it's well-known that there are o(n^3/2) such partitions, not <=n.
In fact you can get that direction in O(n log n). Hint: the match you need to beat is given.
Did you know this solution prior to the contest? Have you seen this paper before? Or did you just use good search-engine skills to find something that could solve the problem?
(I'm asking because I would like to know when it is a good approach to stop thinking about a problem and just google it, especially in an SRM... this could save a lot of time)
I submitted a stupid greedy algorithm in honor of your success in SRM 688. Seems like it doesn't work when I do it :P
It looks like all kinds of heuristic algorithms should be broken with regular 200gon with main diagonals or with "almost main" diagonals. But not to make you sad, I also submitted a heuristic solution and failed systests ;) (second time in a row I was 20min late (but this time it was not TC's fault), but I don't think I would have been able to do this problem even if I wasn't be late)
And one note more, minimum cost matching can be omitted. Since there is line separating parts we can always take two points from different parts which are neighbours on convex hull, match them and recurse. That leads to O(n^3) in total. Combinatorial geometry FTW :)
Hello, may I ask a question about the realization of Div1 1000?
It's that how to divide points into two sets.
In tester's solution, he just iterate through all pair of points (i, j), where i, j is their id, and divide all other points into 2 sets using cross product. But the code writes something like:
I understand that ccw, but what's the point of xoring an (i < j)?
It is the same as
ccw(min(i, j), max(i, j), k). Probably he wants to check the orientation of the ordered (i, j) pair.Thanks!
I don't know where I went wrong in div 2 500 pointer. Can anyone explain his approach ?
You need to consider every possible substring from A with length same as B. Then check whether the substring is a possible match with B. A substring will not match with B if for any index i, substring[i] != B[i]
My screencast