symonsaroar's blog

Inclusion-Exclusion implementation.
By symonsaroar, history, 9 years ago, In English

Problem:

A certain strange mathematician, Rasyak, considers a particular set of prime numbers beautiful. He also calls a composite number beautiful, if it is divisible by at least one prime number in his chosen set of beautiful primes. Given Rasyak’s set of M beautiful primes and an integer N, you have to find the number of beautiful numbers (both primes and composites) between 1 and N. For example, given a set of 2 beautiful primes, {2, 5}, there are 6 beautiful numbers between 1 and 10 (i.e. 2, 4, 5, 6, 8 and 10).

Input
The first line of the input gives the number of test cases, T (1 <= T <= 100). T test cases follow. Each will consist of one line containing a single integer M, followed by a line containing M space-separated prime numbers mi, followed by another line containing a single integer N.
1 <= M <= 25
1 <= mi <= 1000
1 <= N <= 2*10^9

Output
For each test case, output one line containing a single integer X, where X is the number of beautiful numbers between 1 and N.
Input
3
2
2 5
10
3
2 5 13
100
25
2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97
2000000000

Output
6
63
1759360857


I know this can be solved with inclusion-exclusion principle. But,
How do I implement this.
please help me with implementing this in C/C++
It is already in this blog .. but it has only an answer saying about th inclusion-exclusion principle ..

  • Vote: I like it
  • +1
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Auto comment: topic has been updated by symonsaroar (previous revision, new revision, compare).

→ Reply
»
9 years ago, # |
← Rev. 18   Vote: I like it +10 Vote: I do not like it

Initial idea goes like: For each prime p,  there are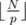 multiples. You find the sum of this over all p. However, some multiples have more than two prime factors so you must subtract this overlap. For example, N = 7, p1 = 2, p2 = 3. Then you have 2, 3, 4, 6 as the multiples. However, if we do 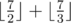we get 5. This is because 6 is counted twice, once for p1 = 2 and again for p2 = 3. To eliminate this overlap, we then subtract 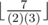from the sum to get 5 - 1 = 4,  the correct answer. Then you add for numbers with three beautiful prime factors, and subtract for numbers with four, until M.

Actually, the above idea is like to time out with 100 test cases unless some smart optimization is used. Perhaps bitmask should be used along with the above ideas to get full solution.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    well, if the limit of m were smaller than 20 .. I can comfortably loop 2^20 times..

    But for the given range(25) I am unable to get in the time limit, as I had to loop 2^25 times..

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      SO, What approach should I use for optimization?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 4   Vote: I like it 0 Vote: I do not like it

        HINT: product of first ten primes  > 109

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it +6 Vote: I do not like it

          GOT AC .. thanks . :D

          → Reply
          • »
            »
            »
            »
            »
            »
            5 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            i need this code

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              5 years ago, # ^ |
              ← Rev. 2   Vote: I like it 0 Vote: I do not like it 
              void solve()
{
    int m;cin>>m;
    int a[m];rep(i,0,m) cin>>a[i];
    int n;cin>>n;
    int o=0,e=0;

    rep(i,1,1<<m)
    {
        int p=1;
        if(__builtin_popcount(i)>=10) continue;
        rep(j,0,m)
        {
            if(i&(1<<j)) p*=a[j];
        }
        if(__builtin_popcount(i)&1) o+=n/p;
        else e+=n/p;
    }
    cout<<(o-e)<<'\n';
}
              → Reply