IlyaLos's blog

Editorial for Codeforces Round #346 (Div. 2)
By IlyaLos, history, 9 years ago, translation, In English

659A — Round House

The answer for the problem is calculated with a formula ((a - 1 + b) 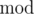n + n) 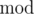n + 1.

Such solution has complexity O(1).

There is also a solution with iterations, modelling every of |b|'s Vasya's moves by one entrance one by one in desired direction, allowed to pass all the tests.

This solution's complexity is O(|b|).

659B — Qualifying Contest

Let's consider the participants from every region separately. So for every region we just need to sort all of its participants by their score in non-increasing order. The answer for a region is inconsistent if and only if the score of the second and the third participant in this order are equal, otherwise the answer is the first and the second participant in this order.

The solution complexity is .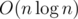

659C — Tanya and Toys

Our task is to take largest amount of toys Tanya doesn't have yet the way the sum of their costs doesn't exceed m. To do that one can perform greedy algorithm: let's buy the cheepest toy Tanya doesn't have at every step, while the amount of money left are sufficient to do that. The boolean array used can be a handle in that, storing true values in indices equal to toy types which Tanya does have at the moment. As soon as 109 money is sufficient to buy no more than 105 toys 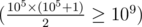, used is enough to be sized 2 × 105 (we won't buy the toys with types numbered greater). So we just need to iterate over the number of type we want to buy, and if corresponding value in used is equal to false, we should buy it, otherwise we can't.

The solution complexity is .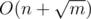

One can use the <> data structure (C++ \texttt{std::set}, for example), for storing the types Tanya has at the moment. In this case the complexity is .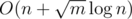

659D — Bicycle Race

From the track description follows that Maria moves the way that the water always located to the right from her, so she could fall into the water only while turning left. To check if the turn is to the left, let's give every Maria's moves directions a number: moving to the north — 0, moving to the west — 1, to the south — 2 and to the east — 3. Then the turn is to the left if and only if the number of direction after performing a turn dir is equal to the number before performing a turn oldDir plus one modulo 4 .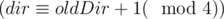

This solution has complexity O(n).

One can solve this problem in alternative way. Let the answer be equal to x (that means that the number of inner corners of 270 degrees equals x, but the number of inner corners of 90 degrees to n - x). As soon as the sum of the inner corners' values of polygon of n vertices is equal to 180 × (n - 2), then x × 270 + (n - x) × 90 equals to 180 × (n - 2). This leads us to 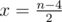, being the answer for the problem calculated in O(1).

659E — New Reform

One should notice, that for every connected component of the graph the problem could be solved independently, so we just need to solve the problem for any connected graph.

Let this connected graph (of n vertices) contain n - 1 edge (such is called a tree). If one maintain a DFS from any of its vertex, every edge will be oriented, and each of them could given to its ending vertex, this way every vertex (except the one we launched DFS from, that is the root) will be satisfied by an edge. In this case the answer is equal to 1.

Let's then deal with a case when the graph contains more than n - 1 edges. This graph contains at least one cycle. Let's take arbitrary vertex from any of the cycles and launch a DFS (as above) from it. All vertices except chosen will be satisfied, so we are to give an edge to the chosen vertex. As soon as chosen vertex belongs to a cycle, at least one of its edge will not be taken to account in the DFS, so it can be given to a root. This way all the vertices will be satisfied.

Now we are able to solve the task for any connected graph, so we are to divide the graph into a connected components — this can be easily done by DFS or BFS.

The solution complexity is O(n + m).

659F — Polycarp and Hay

In this task one should find a connected area, in which the product of the minimum value of the cells and the number of the cells is equal to k. To find such, let's sort all the n × m cells by their values by non-increasing order. Then we will consecutively add them in this order one by one, maintaining a connected components on their neighbouring relations graph. It's enough to use Disjoint Set Union structure to do so, storing additionally size of every component.

Let ai, j be the last added element in some component id, so ai, j has the minimum value among all the cells in component id (according to our ordering). If ai, j does not divide k, then the component id could not consist of desired area. Otherwise (ai, j is divisor of k), let's find need = k / ai, j — desired area size (if it contains ai, j), and if CNTid is not less than need, then the component id contains desired area, which could be easily found by launching a DFS in a neighbouring relation graph from ai, j, visiting only the ap, q ≥ ai, j and exactly need of them.

The solution complexity is .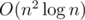

659G — Fence Divercity

Let the answer for the problem be the sum

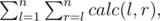
where calc(l, r) is the number of ways to cut the top part of the fence the way its leftmost part is in position l and the rightmost in position r. If l = r, that is the case when the cutted top part consists of part of only one board, then calc(l, r) = hl - 1.

Let r > l, then

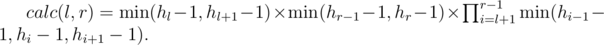
In other words, the number of ways to cut the top part of some board is equal to minimum value among heights of it and its neighbours minus one, otherwise the cutted part will be inconsistent. Leftmost board and rightmost board are considered separately, because each of them does have only one neighbouring board. So the answer looks like

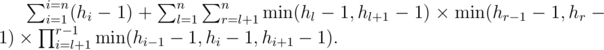
The first summand is easy to calculate, so let's take a look at the second. Let us modify it as the following:

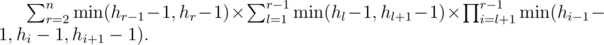
Let

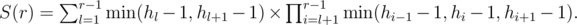
Let's take a look how does the S(r) change after increasing r by one:

S(r + 1) = S(r) × min(hr - 1 - 1, hr - 1, hr + 1 - 1) + min(hr - 1, hr + 1 - 1).

This way this sum is easy to maintain if consecutively increase r from 2 to n.

The solution complexity is O(n).

  • Vote: I like it
  • +85
  • Vote: I do not like it

Comments Comments (77)
| Write comment?
»
9 years ago, # |
  Vote: I like it +70 Vote: I do not like it

Thanks for nice problems и fast Разбор

→ Reply
»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Thanks for the lightning speed EDITORIAL.

→ Reply
»
9 years ago, # |
  Vote: I like it +7 Vote: I do not like it

In F problem, I haven't seen the limit that must have an unchanged cell... So I wrote a code in O(sqrt(min(k, 1e15)).. When k > 1e15 print "NO", then enumerate the factor of k, use dsu to solve it, and got WA4. After contest I found the limit and add it then accepted...sad..

→ Reply
»
9 years ago, # |
  Vote: I like it +20 Vote: I do not like it

The best contest i've seen so far, I really liked the problemset and the fact that is was a 7 problem round instead of the regular one. Great job!

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

why this 17050130 gets WA in problem E?!!

any one can provide a small case which make it fail ?!

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Problem should be solved for every component independently.

    6 6
1 2
2 3
3 4
4 1
1 3
5 6
    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +7 Vote: I do not like it

    I believe this input is a small one where your program fails. There are two connected components: one is a tree and the other is a super well-connected component. The main idea for this test is that the degrees for some vertices are large enough so that when you subtract m edges, then you will not end up with any zeros.

    10 13
1 2
1 3
1 4
1 5
1 6
2 3
3 4
4 5
5 6
6 2
7 8
8 9
9 10
    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +26 Vote: I do not like it

      Yea, you don't need to read other comments, better post the same idea that i've already posted but with two times bigger test, good job.

      → Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

I feel guilty for doing this 17058751 for 659D - Bicycle Race:

  • I simply used java.awt.Polygon class to create the lake polygon.

  • If Maria misses turn i, she would proceed by dx = signum(x(i) - x(i+1)), dy = signum(y(i) - y(i + 1))

  • Then I simply checked if lake polygon contains (x(i) + 0.5*dx, y(i) + 0.5*dy)

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +9 Vote: I do not like it

    Well i guess that's still more ethical than "cout<<(n-4)/2";

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can anybody explain why that is correct?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        No idea

        → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +6 Vote: I do not like it

        It's all explained in the editorial, but:
        - assume that for all polygons (convex or concave) the sum of internal angles is 180(n - 2)
        - for this problem, there are only internal angles of 270º and 90º and we need to count how many (x) of the former ones exist:

        180(n - 2) = 270x + 90(n - x)
        → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I used ray casting with the same approach...

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    One line code for problem D using Point2D.relativeCCW()

    submission

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Hello everyone , Why testcase 53 is not correct in my answer since my answer totally matched with jury answer here is the link... for problem 2

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You have to check if vec[i].size() > 2 before accessing the third element via vec[i][2]. Otherwise you may access unallocated memory. I made the same mistake...

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Why does this only seem to fail on test 53? Even the first test case has a region with 2 people.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Suppose size is 2. Then suppose that vec[i][0] = vec[i][1]. Then you will look for vec[i][2] to compare with vec[i][1], but that element might not exist (causing Runtime Error). In samples vec[i][0] > vec[i][1], so you didn't need the third element.

        → Reply
»
9 years ago, # |
  Vote: I like it +6 Vote: I do not like it

There is a parsing error in the editorial of F

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I solved D by finding point inside a polygon . I had to code almost from the scratch because somehow geeksforgeeks code was not working -_- . And after seeing this O(1) solution.....

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Happened with me too !
    I found a working code though ( around 7 lines ) 

    int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy)
{
  int i, j, c = 0;
  for (i = 0, j = nvert-1; i < nvert; j = i++) {
    if ( ((verty[i]>testy) != (verty[j]>testy)) &&
	 (testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )
       c = !c;
  }
  return c;
}
    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anybody tell me why i have a WA in test 15 of problem B?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    The problem is where you print the answer.

    When there are only 2 people in a region the if statement access an irregular position in memory.

    → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Hello,

    sure, it is because you forgot to check size of vector

    make the checking line:

    if (v[i].size()<3u||v[i][1].p != v[i][2].p)

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Could anyone help me with that http://codeforces.me/contest/659/submission/17057892 ?

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

My solution for problem D is to count the number of left turn and the number of right turn then take the minimal of them. I have no idea why it works. It was a desperate attempt. Can somebody provide a proof? Thank you!

My submission: http://codeforces.me/contest/659/submission/17055311

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    My guess is number_of_right_turns = number_of_left_turns + 3

    So number_of_right_turns is always greater than number_of_left_turns.

    You are actually taking number_of_left_turns.

    Just cout << posi << endl; also get AC.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain problem F in more detail please? Basically for each cell with value v, you want to know C(v) = how many cells are connected to it that are at least v. When you sort by decreasing value and DSU, won't your calculation of C(v) for cells with the same value be wrong? For example this grid:

2 4 5

6 4 3

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I didn't notice that in problem D we may only drop into water on left turn and solved the more generalized version of the problem.

The idea is we can record all the vertical and horizontal segments, and for each turning point we can count how many segments we may intersect if we keep going straight. If the count of segments is odd then this point is dangerous, and not while the count is even.

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How does that formula come in problem number A ? Can somebody illustrate please ?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Forget the formula. Basically, all you need to do is to make a loop. When the system has 5 rooms, going 6 rooms front actually means going 1 room front, right? For backward movement, 2 rooms back means 3 rooms front. Just keep adding the number of total rooms until you get a non negative number. So taking mod is enough. Just to avoid 0'th position, as 5%5 or 6%6 makes zero, but you want to print 5 or 6, the mod operation is done in two steps. Eventually the -1 with a and the +1 at the end don't make any difference.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In 2nd Problem, why is the output on terminal and Codeforces Judge different??

I got WA on 1st pretest again and again because of this..

My solution is :- http://codeforces.me/contest/659/submission/17065952

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    1) You are doing ios_base::sync_with_stdio(0);

    2) Then read something C-style: scanf("%d %d",&n,&m);

    3) Then read something C++-style: cin>>str>>reg>>score;

    Due to 1), 2) and 3) both read same data. I.e. in 3 you read very first input line instead of second.

    → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Hello for problem D, I have a doubt what property does this test case violate:

5
1 1
1 2
-1 2
-1 1
1 1
→ Reply
»
9 years ago, # |
  Vote: I like it +3 Vote: I do not like it

First of all, thank you for the quick editorial!! I would like to mention 2 points regarding the editorial:

  1. The phrase "as soon as" is used in places where "since" or simply "as" should be used. It is not that important(since the intention is very much clear), but feels odd! :P

  2. For problem E, I did not understand the part "...as chosen vertex belongs to a cycle, at least one of its edge will not be taken to account in the DFS, so it can be given to a root. This way all the vertices will be satisfied." clearly. Can someone explain it in more details?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It is perhaps slightly misworded. The key idea is that for any tree, we can pick any root and direct each of the edges so that only the chosen root of the tree is unaccessible. Therefore, if the program finds a cycle in a connected component, and we assign the root to any node of the cycle then one can perform the same algorithm, except this time there will be one extra edge incident to the picked root (otherwise, the cycle wouldn't exist). This extra edge can, of course, be directed to make the root accessible as well, thereby solving the problem.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      So, in short, does this mean the following?

      1. The final answer is the sum of the answers for each individual connected component.

      2. For a connected component, the answer is 1 if the component is a tree, 0 otherwise.

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can any one tell why am i getting RTE on problem B

this my submission

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Good day to you man!

    The RTE is because of sort :'( you have to change comparator:

    bool cmp(pair<string, int>s1, pair<string, int> s2) {
    if (s1.second >= s2.second)
        return false;
    return true;
}

    like this :)

    +btw I'm convinced the part at the end is also wrong :/

    I would change it like:

    REP(i, 1, m + 1) {
        int size = mat[i].size();
        if (size==2||mat[i][size - 2].second != mat[i][size - 3].second) {
            size--;
            if (size - 2 >=0 ) {
                if (mat[i][size - 1].second != mat[i][size - 2].second) {
                    cout << mat[i][size ].first << " " << mat[i][size - 1].first << endl;
                    continue;
                }
            } else {
                cout << mat[i][size ].first << " " << mat[i][size - 1].first << endl;
                continue;
            }
        }
        cout << "?" << endl;
    }
    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thnx !! it worked !! but i can't understand why RTE ?!

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Well, sort comparator must be deterministic.

        That means it must decide (in finite time) for each pair of elements, whether one of them is bigger (and which one) or whether they are equal.

        a: A < B && !(B < A) means A < B

        b: !(A < B) && B < A means A > B

        c: !(A < B) && !(B < A) means A == B

        anyway A<B && B<A (which could have been returned in your program) is "nothing" so the function could not determine, how to sort it :)

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain solution for F in more details ?

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem G has a divide and conquer solution too ... :P *I wanst able to arrive at the formula stated in the editorial but divide and conquer was a bit more intuitive to me *

Link to submission- http://codeforces.me/contest/659/submission/17075860

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can anyone explain solution of problem E in detail.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Every connected component of the graph, could be solved independently. Each connected component has at most 1 vertex with ending degree 0 after all (solving optimally) . If the connected component is a simple path or a tree root on a vertex v, we may notice that this component has 1 vertex with ending degree 0. If the connected component is cyclic, starting on any node we can organize the Edges in order to take no edges with ending degree 0. Imagine we have one conected component witch has a cycle and a path or a cycle and a tree or both :) , for example this: 1-2, 2-3, 3-1, 1-5, 5-6; Notice we can turn it into the problema of the cyclic connected componen. For this, we can also pick the vertex with in-out degree=1 and connect it. For example: 1-2 , 2-3 , 3-1, 1-5 5->6; 1-2,2-3,3-1, 1->5, 5->6; In this phase we have the same cycle! Therefore, we can run a dfs for each connect component and verify if it has any cycle. If it has add the answer by 1, if it has not, add the answer by 0.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      If it has a cycle, we should not add 1 to the answer right? your last two lines confuse me

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Sorry! You are right! if it has a cycle, we should NOT add 1 to the answer :)

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Thanks. Some beautiful problems and elegant solutions out there. :)

→ Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

There is O(1) solution for problem E. http://www.codeforces.com/contest/659/submission/17067296 Can anyone explain me this.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    It's not a real solution. It exploits the fact that many tests cases share the same solution and compares number of nodes, edges and first number in second line to identify the test case and print the solution accordingly.

    You can easily hack it! ;)

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Means it has weak test cases.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Not necessarily, however, if the problem statement asked to print unreachable nodes it would be way more easier to solve it properly

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Please it would be really grateful if someone can explain editorial of Problem F.

→ Reply
  • »
    »
    9 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    You just need to launch dfs from all i and j that k % a[i][j] = 0 and k / a[i][j] <= n * m. In dfs count values that v >= a[i][j]. if value equals to k / a[i][j] you could find answer.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Thanks I got your point but if we launch dfs from each i and j for the mentioned condition, won't the complexity be O(n*m*(n*m)) in worst case? How to make it efficient?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You will mark every used points. You can see my solution here

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Thanks lord, I didn't realized that the maximum distinct divisors we have to check is really small as n*m<=1e6

          → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem G

please explain how S(r + 1) = S(r) × min(hr - 1 - 1, hr - 1, hr + 1 - 1) + min(hr - 1, hr + 1 - 1).

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem E

why N — BPM getting WA?

Graph :

Edge 1 | Node1

Edge 2 | Node2

Edge 3 | Node3

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Sorry, I am too late but in problem E, what about individual components with no roads why we have to add 1 as I was getting WA earlier but question states a city is separate only when it has no road leading into it and only leading out of it.

→ Reply
»
14 months ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

My hand at a more "human" explanation for problem G from someone bad at maths:

First, let's solve this task for constant h[i] (assuming each element of h is reduced by 1 from now on).

If we only consider the first plank, we can cut off any part of plank 0 from 1 to h[0]. The total answer for this plank is h[0] — dp[0] = h[0].

If we consider the second plank, we can either only cut off part of plank 1 from 1 to h[1], or do the same in addition to any possible cutoff ending at the previous plank (it's clear that no matter whether we cut off 1 or h[1], we still can cut off any part of h[0]). The answer for this plank is h[1]+h[1]*h[0], and the total answer is h[0]+h[1]+h[1]*h[0].

We can advance infinitely, storing the answer for the previous plank:

dp[i] = h[i] + h[i] * dp[i-1]
ans = sum(dp)

Now let's consider the case where h[i] is non-decreasing.

The start is obviously the same, but things change starting from the second plank.

If we want to cut h[1] but leave h[0] (and everything before) as-is, nothing changes for us, so h[i] is still part of dp[i].

But if we want to also cut off part of h[0] and h[0] < h[1], then we can only cut off any part of h[0] if we also cut h[1] to the same height as we will cut h[0]. For example, if h[0] = 3 and h[1] = 10, we can cut h[0] and h[1] to length 0, length 1 or length 2, but cutting h[1] to length 3 makes h[0] impossible to cut.

This means that in this case:

dp[0] = h[0]
dp[i] = h[i] + min(h[i], h[i-1])*dp[i-1]
ans = sum(dp)

Finally, let's consider the hardest case — non-increasing sequences.

If we want to cut off h[0] alongside h[1] and h[0] > h[1], then we can only cut h[0] to the same or smaller height as h[1]. If h[0] = 10 and h[1] = 2, we can cut h[1] to 0 (in which case h[0] must be cut to 0 as well), or we can cut h[1] to 1 (in which case h[0] can be cut to either 0 or 1). In addition, all options that depend on h[0] being higher than h[1] are unreachable from h[1].

So in this case, only part of dp[i-1] must be used — instead of dp[i-1], use the same formula as before dp[i-1] but with changed height:

calc_dp(0, height) = height
calc_dp(i, height) = height + min(height, h[i-1]) * calc_dp(i-1, min(h[i-1], h[i]))
dp[i] = calc_dp(i, h[i])
ans = sum(dp)

Or, to put it in a different way:

# h2 is needed to account for increasing sizes (h[i]<h[i+1])
h2[i] = min(h[i-1], h[i])
# dp2 is needed to account for decreasing sizes
# dp2[i]: how many options ending at plank i are reachable from plank i+1
dp2[0] = h2[1]
# specifically min(h2[i], h[i+1]) on the next line is needed to account for decreasing sizes, otherwise dp2 is equivalent to dp
dp2[i] = h2[i+1] + dp2[i-1] * min(h2[i], h[i+1])
# dp[i]: how many options end at plank i
dp[0] = h[0]
dp[i] = h[i] + dp2[i-1] * h2[i]
ans = sum(dp)

Still pretty convoluted, but hopefully a bit easier to understand. See 223426302

→ Reply