→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
16:47:54
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
16:47:54
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 30.11.2024 00:47:06 (l2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











Могу предложить такое решение:
Сгенерируем все делители m. Сделаем бинпоиск по ответу. Переберем a = gcd(i, m) (видим, что a — делитель m), теперь осталось понять, сколько существует таких i = ac и j таких, что Запрос для i сводится к запросу "сколько чисел от 1 до h взаимно просты с m" (где
Запрос для i сводится к запросу "сколько чисел от 1 до h взаимно просты с m" (где 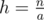 ), ответ на запрос для j просто
), ответ на запрос для j просто 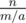 . Для запроса на i можно применить формулу включения-исключения по простым делителям m. Различных простых делителей не больше 9, поэтому решение работает за
. Для запроса на i можно применить формулу включения-исключения по простым делителям m. Различных простых делителей не больше 9, поэтому решение работает за 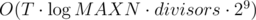 . Делителей у числа до 109 может быть порядка тысячи, поэтому такое решение должно заходить.
. Делителей у числа до 109 может быть порядка тысячи, поэтому такое решение должно заходить.
1) Заметим, что чем больше n, тем больше нулей в таблице. Можем использовать бинарный поиск по ответу.
2) Теперь у нас есть фиксированное n, нужно посчитать количество нулей для него. Зафиксируем номер строчки i, можно увидеть, что ответ для нее — результат целочисленного деления n на величину (m/gcd(m, i)). Нам нужно найти сумму этой величины по всем i.
3) Единственное что меняется в той формуле при смене i — значение gcd(m, i). Давай посчитаем, сколько есть чисел в промежутке 1 до n с фиксированным gcd (различных gcd — ). Зафиксируем очередной делитель m — d[i], для него ответ равен n/d[i], но из этой величины нужно вычесть сумму ответов по всем d[j] таким, что d[j] делится на d[i]. Эту часть, думаю, можно сделать проще принципом включений-исключений, но я не знаю как.
). Зафиксируем очередной делитель m — d[i], для него ответ равен n/d[i], но из этой величины нужно вычесть сумму ответов по всем d[j] таким, что d[j] делится на d[i]. Эту часть, думаю, можно сделать проще принципом включений-исключений, но я не знаю как.
И того, вышло решение за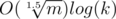 ), это около 30 миллионов на один тест.
), это около 30 миллионов на один тест.
UPD: Опередили, но у меня вроде бы немного другое решение
Там должно быть log(max(k, m)), а не log(k). Но это не влияет на асимптотику.
Kostroma, Fcdkbear спасибо :)