farnasirim's blog

"Center" of a set of points
By farnasirim, history, 9 years ago, In English

Hi.

As always the question can be stated fairly easily:

Given a set of points on a 2D plane, how to find a point (x, y) on that plane such that sum of the euclidean distances between the chosen point and the given points is minimum (among all possible choices of (x, y))?

How about finding the same thing in a 3-Dimensional space?

Thank you for the time you put on reading this and thanks in advance for sharing your solution/idea.

  • Vote: I like it
  • +21
  • Vote: I do not like it

»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I misunderstood the problem, Ignore

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    because you don't care about the points inside the CH

    wtf?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I meant you don't care about the points in the set which are inside the convex hull.

      It's so because the diameter will always be a pair of the Convex Hull's vertexes.

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it +20 Vote: I do not like it

        But the diameter has nothing to do with the problem in this entry...

        → Reply
        • »
          »
          »
          »
          »
          9 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          Lol, just understood that I misunderstood the problem :D

          Sorry the solution is to a completely different problem.

          → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +35 Vote: I do not like it

    You minimize the maximal distance between the center but not the sum of them. The solution of the original problem is to run two ternary searches: on x and y coordinates, one into another. The proof is based on the fact that the sum of the convex functions is a convex function.

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Should the two ternary searches be independent or should they be nested?

      → Reply
      • »
        »
        »
        »
        9 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        When in the first ternary search you fix some x, then you run ternary search on y in fact on the segment [(x,  - ∞), (x,  + ∞)].

        → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why is simple ternary search the bad idea?

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    This would mean that the point we are looking for is (x, y), where x and y are the "center"s of the projection of the set of points onto the x axis and y axis respectively. Right? Can you prove the correctness?

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      Distance to some point is convex function. Sum of convex functions is also a convex function. Isn't it enough?..

      → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

This point is called Fermat-Weber point. For n=3 we get famous Torricelli point. But in my opinion for other n it is #P complete problem.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +23 Vote: I do not like it

    But anyway, for each ε there exists an algorithm polynomial on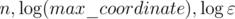 , finding the point with precision ε. I think that for ε = 0 you simply can't output precise answer, when it is irrational, so I don't think we can consider this problem as a #P problem, or we need to find a way to express the answer in the other form.

    → Reply
»
9 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What if we want to find one of the given points that have minimum sum?

→ Reply