
С 26 марта по 28 апреля 2016 года пройдет VI Открытый чемпионат БГУИР по программированию (г. Минск, Беларусь).
К участию в Чемпионате приглашаются студенты и магистранты БГУИР, учащиеся общеобразовательных учреждений, студенты других вузов и стран СНГ.
Соревнование пройдет в 3 этапа:
- первый отборочный тур (заочный четвертьфинал, условия задач на русском) — 26-29 марта;
- второй отборочный тур (очно-заочный полуфинал, условия на русском и английском) — 5 апреля;
- финал Чемпионата (очный, только английские условия задач) — 26-28 апреля.
Первый отборочный тур обязательный только для команд БГУИР и школьников, но другие команды также могут принять участие. Второй отборочный тур обязателен для всех команд; команды БГУИР и школьников г. Минска, прошедшие первый отборочный тур, участвуют в нем очно, остальные заочно.
Для участия в Чемпионате необходимо зарегистрировать команду участников до 03.04.2016 (до 28.03.2016 для студентов БГУИР и школьников). Оргвзнос за участие отсутствует — участвуйте в свое удовольствие.
В финал проходят 42 команды, показавшие лучшие результаты во втором отборочном этапе, но не более:
- 7 команд студентов и магистрантов БГУИР;
- 5 команд школьников (по одной команде от каждого среднего общеобразовательного учреждения);
- 2 команд от каждого вуза Республики Беларусь и стран ближнего и дальнего зарубежья.
Открытый чемпионат БГУИР по программированию проводится по правилам ACM-олимпиад. В финале соревнования участникам предлагается от 8 до 12 заданий, которые следует решить за 5 часов. Задачи сформулированы на английском языке.
Более подробную информацию о Чемпионате, а также условия задач и результаты прошлых лет можно найти на портале acm.bsuir.by. И немножко видео с прошлого года:
UPD Трансляция финала доступна по ссылке.











Автокомментарий: текст был обновлен пользователем aropan (предыдущая версия, новая версия, сравнить).
Первый отборочный тур уже стартовал. Условия здесь, а результаты здесь. Напомним:
Если не секрет, с чем связано то, что и полуфинал, и финал проходят в рабочие дни? Кажется, что многим командам это может быть не очень удобно.
Я подозреваю, что полуфинал и финал проходит очно и есть некоторые сложности со сбором большого количества людей в университете в выходной день.
Как решать задачу B с полуфинала?
Откройте дорешку!
Дорешивание открыто
..., пожалуйста.
Кто сдал в F решение за O(NM)? Мы налажали с ориентацией ребер.. и получали Wa12, а потом отправили простой bfs, так как дофига команд сдало задачу, с очень красивой идеей. Нам показалось странным.
P.S Откройте дорешку!
Я думаю, что большинство сдали либо NMlog как мы, или просто четвертую, которая тоже проходила.
UPD: По предположениям некоторых, это даже не четвертая.
Спасибо за контест, очень понравилось, задачи были на всевозможные темы, приятно было порешать)
Очень интересно узнать авторское к задаче про ханойские башни, учитывая, что "Хотя вариант с тремя стержнями имеет простое рекурсивное решение, оптимальное решение Ханойской башни с четырьмя стержнями является нерешённой проблемой." (из википедии)
Ну мы предположили следующее, что ответ для n, строится как мы сначала перекладываем при помощи всех 4 стержней сколько-то дисков сверху, а потом оставшиеся с помощью 3 стержней, в итоге dp[n] = min(2 * dp[k] + 2 ^ (n — k) — 1) по всем k = 1..(n-1), а дальше просто увидели закономерность.
Предположили — это, конечно, супер, но мне интересна мотивация авторов давать задачи, решение к которым никто не умеет доказывать.
Ну я предполагаю, что авторы всё таки имеют доказательство этой задачи, ну или хотя бы надеюсь на это)
Тогда им, видимо, стоит написать с ним сенсационную научную статью unless вики врёт.
На английской википедии есть вот такая фраза: "There is also a "presumed-optimal solution" given by the Frame-Stewart algorithm, discovered independently by Frame and Stewart in 1941. The related open Frame-Stewart conjecture claims that the Frame-Stewart algorithm always gives an optimal solution. For the case of four pegs it was proven by Bousch in 2014 that the Frame-Stewart algorithm is optimal."
Кажется, что для случая с четырьмя стержнями все как раз таки доказано, а вот для больше го количества уже проблемы. Сам алгоритм вроде делает ровно то, что было написано выше.
Даже если так, давать задачи, решение к которым можно только угадать — сомнительное дело.
Ну вроде зачастую встречаются задачи, которые опираются на нетривиальные факты, такие что самому их доказать почти невозможно(по крайней мере не за контест)
Да, встречаются. ИМХО, в большинстве случаев это неправильные задачи, которые вообще не стоит давать на контесты. Как исключение — идеи, которые входят в некий общепризнанный ликбез и задачи, сделанные для того, чтобы ознакомить сообщество с чем-то новым. Последние, впрочем, опять-таки, как мне кажется, не должны встречаться на "официальных" соревнованиях. Максимум — на раундах в online judge или на тренировочных сборах.
Ну да, согласен, всегда не приятно встречать такие задачи, но что поделаешь, наше дело решать)
Что кто сдал в С?
У нас была идея — перебрать правую половину массива, сохранить возможные четности правых половин отрезков, проходящих через центр и для каждого набора четностей выбрать наилучший набор, на котором она достигается. Потом перебрать левую половину массива, посчитать, какие четности мы ожидаем от правых половин отрезков, проходящих через центр и выбрать подходящий для них вариант. Ну и да, ответ считать состоящим только из 0 и 1.
К сожалению, не отдебагали.
А что вы в H сдали?
количество единиц в двоичной записи чётно
чётно  сумма количеств единиц в двоичных записях a и b четна. Таким образом, задача сводится к подсчёту чисел на отрезке, у которых количество единиц в двоичных записях нечётно. Мы это делаем такой функцией:
сумма количеств единиц в двоичных записях a и b четна. Таким образом, задача сводится к подсчёту чисел на отрезке, у которых количество единиц в двоичных записях нечётно. Мы это делаем такой функцией:
Мы сдали примерно такое.
Построим граф, вершины — это префиксы искомого массива, ребра 2х типов — "(не)равны по модулю 2". Соответственно, сожмем по ребрам равенства, остальное надо покрасить в 2 цвета. Понятно, что в каждой компоненте 2 варианта раскраски. Ну просто переберем это.
Чтобы это работало быстро, нужен еще один небольшой хак. Заметим, что изолированные вершины (те, у которых нет ребер ни одного из типов) могут быть какими угодно, значит, можно их не перебирать, а просто поставить их такими, чтобы в конце был 0, в зависимости от значения префикса на 1 короче. Очевидно, что после сжатия и удаления таких вершин у нас будет
Unable to parse markup [type=CF_TEX]
компонент, так как каждой компоненте соответствует ≥ 2 изначальные вершины. Итого получаем что-то околоUnable to parse markup [type=CF_TEX]
.По С есть такая интересная идея. Давайте перебирать по порядку элементы ответа. Пусть в первом элементе будет ноль. Тогда чуть модифицируем отрезки которые задают условия. Теперь у нас есть какие-то условия, и нам нужно ответить есть ли такие значения переменных, при которых они выполняются. Если решения нет, значит ноль брать нельзя и возьмем единицу. Это очень натурально можно представить в виде системы уравнений по модулю 2, которую можно решать допустим гауссом. Итого решение за n^4. Это хуже авторского, но легко в понимании.
UPD: да, действительно, забыл про первоочередность минимальности суммы.
А каким образом при этом добиться минимизации суммы, которая приоритетнее лексикографической?
Контрпример.
Input:
3 2
1 2 1
2 3 0
Output:
1 0 0
Описанное решение даст ответ 0 1 1. Кстати, проверка совместности при подстановке нуля — в точности задача Timus. 1003
P.S. Хуже авторского? А оно что... Полиномиально? О_О
А кто-нибудь умеет в D доказывать, что рандом достаточно быстро отрабатывает?
Прикольно.. ну не знаю, как рандом. .мы просто старались более равномерно всех живых раскидать.
Можно подробнее, какой рандом? Мы просто шли в число, где максимально возможное количество новых вариантов будет минимально...
Ну я поддерживал множество текущих вариантов и каждый раз брал случайно элемент множества, считывал ответ и выкидывал то, что под него не подходит. Зашло :)
Можно честно найти такой сид, запустить на нем все тесты и убедиться.
Мы каждый раз спрашивали первое число, которое не противоречит уже полученным ответам. Умеете такое ломать?
Вроде в таком случае 5293 не должно проходить.
Проверил вашу посылку — валится на этом тесте. Просто в наборе тестов его не было.
Действительно. Непросто сделать на online judge'е все 5040 тестов без группировки. :)
Ссылка на условие есть у кого-нибудь?
link
Кто из участников, сдававших BFS не за чистый O(NM) в F, умеет оценивать сложность, и говорить, что это лучше
Unable to parse markup [type=CF_TEX]
?Ну у меня вроде NM log
Будем обрабатывать в порядке уменьшения c, поддерживая вместо стандартной BFS-овской очереди сет. Когда достаем очередную вершину, помечаем ее как подожженную и в случае необходимости (то есть если соседи должны загореться, но еще не помечены как горящие) добавляем в сет соседей. Понятно, что если вершину достали из сета, то больше она туда попасть не может, потому что она уже помечена как горящая, и при этом помечена с максимально возможным c в силу порядка обработки вершин.
А в чем проблема? Говорим, что у нас граф (X, Y, C) — клетка (X, Y) будет гореть еще C секунд. Про С можно сразу сказать, что оно не превышает N + M. Вот и получаем состояний NxMx(N + M), а переходов того же порядка.
Паша, Предствавь змейку.. тогда C нужно делать порядка NM. Или у вас если C большое заменить на N + M зашло?
Зашло по сути в лоб: закинуть сразу всех в очередь, а потом не добавлять новую вершину в очередь или не добавлять соседей текущей если мы уже знаем, что можно туда попасть с бОльшим C. То есть похоже на то, что urusant написал выше, но без сетов.
Но сейчас я уже тоже понял, что не так уж и понятно за сколько оно работает. Почему-то на контесте показалось, что это будет NxMx(N + M) по таким вот соображениям, особенно когда её начали сдавать :)
Кто-нибудь писал в задаче К не корневую декомпозицию, если да, то интересно было бы увидеть решение.
Расскажите A?
Для удобства назовем подпоследовательность массива b хорошей, если соответствующая подпоследовательность массива a является возрастающей.
Пусть g(d) — количество хороших подпоследовательностей c НОД кратным d. Пусть h(d) — количество хороших подпоследовательностей c НОД равным d. Тогда ответ на задачу будет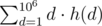 .
.
Заметим, что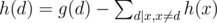 . Мы должны будем от g(d) хороших подпоследовательностей c НОД кратным d отнять все хорошие подпоследовательностей с НОД больше чем d и кратным d. Пусть f(d) — это коэффициент перед g(d) в ответе. Посчитаем значения f(d).
. Мы должны будем от g(d) хороших подпоследовательностей c НОД кратным d отнять все хорошие подпоследовательностей с НОД больше чем d и кратным d. Пусть f(d) — это коэффициент перед g(d) в ответе. Посчитаем значения f(d).
Возьмем делитель a числа d. Заметим, что все g(d) хорошие подпоследовательности с НОД кратным d, также входит в список хороших подпоследовательностей с НОД кратным a. Так как коэффициент перед g(a) равна f(a), то мы должны f(a) раз отнять g(d). Тогда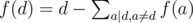 . Отсюда следует, что f — функция Эйлера. Ответ будет равен
. Отсюда следует, что f — функция Эйлера. Ответ будет равен 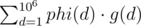 .
.
Для каждого d в векторе будем хранить все числа ai таких, что bi кратно d. И в каждом векторе отдельно посчитаем количество возрастающих подпоследовательностей. Итоговая асимптотика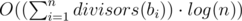 .
.
Трансляция финала доступна по ссылке.
Крутая идея, Лёха! Молодцы :)
Просьба к участникам финала пока не обсуждать условия задач здесь.
Дорешивание задач финала будет открыто примерно через 0.42 секунды)
А фотки с финала такие же как и с полуфинала.
Исправили. Будут дополняться.
А можно запись разбора?
Где можно посмотреть таблицу результатов ?
Результаты финала