
English version
Find all prime numbers between N and M, with 0 < N < M < 1025.
A further classification said that the time limit is 1 second and M - N < 109.
I'm wondering if there is a solution for this problem.
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | jiangly | 3976 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3482 |
| 8 | hos.lyric | 3382 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3357 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | -is-this-fft- | 165 |
| 3 | Um_nik | 161 |
| 3 | atcoder_official | 161 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 147 |

English version
Find all prime numbers between N and M, with 0 < N < M < 1025.
A further classification said that the time limit is 1 second and M - N < 109.
I'm wondering if there is a solution for this problem.
| Название |
|---|



I'm not sure but I don't think there is a solution to this problem for 3 reasons.
1-) It is obvious that we can't iterate over those M-N numbers. It would be 5 * 108 by itself which would exceed 1 sec. run time limit.
2-) Since the numbers are too large we can't use prime sieves either, at least the ones I know.
3-) Even though we find the prime numbers in 0 sec, I assume we won't be able to print them out in 1 sec since there are probably more than 107 prime numbers between N and M in the worst case.
It would be great if someone can find a solution though.
And the main problem is to find prime numbers between 2 strings because of large numbers
maybe
BigInteger.nextProbablePrime()in java will work? not sure, though.But we should use Pascal
The algorithm behind is Miller-Rabin primality test , so you need to implement it yourself
Miller Rabin will probably be too slow. By the Prime Number Theorem,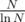 primes exist below N, and Miller Rabin runs in
primes exist below N, and Miller Rabin runs in 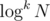 or something. Even assuming k=1, this means it will take O(N) where N = 1e9. I think you have to find each prime in constant time somehow.
or something. Even assuming k=1, this means it will take O(N) where N = 1e9. I think you have to find each prime in constant time somehow.
It is not enough, either.
Well, it would definitely speed up the process but unfortunately not enough.
With that function or the algorithm behind it, we still need to check primality of the returned numbers. That means the time complexity is O(primalitytestcomplexity * 107) in the best case when M - N = 109. I don't think there is a primality test with a time complexity of less than O(log2N)
http://www.wolframalpha.com/input/?i=prime+numbers+less+than+10^9
There are 50000000+ primes under 10^9 :( simply printing these will be a big challenge.
Actually the 2nd and 3rd problems in this paper were very easy, so I am quite sure that this problem was having some mistakes, or the actual tests' limits are small enough to brute force. Anyway this is the Vietnamese problems' style nowadays.
Maybe use range sieve. It will require about sqrt(M) + (M-N) operations and bits of memory, even with inf memory this will take >> than 1 sec
Usually the trick to do well in middle school level competitions in Vietnam is to just ignore the unrealistic constraints.
Wow, please explain to me why this problem it's too big limits?
koosaga has already said: There are 50000000+ primes under 10^9 :( simply printing these will be a big challenge.
This problem is (probably) impossible to be resolve.
As you can see, I wrote a program 24418001 to print integer from 1 to 50000000 here and submit to a random problem and got TLE(more than 2 second while the time limit here is 1 second).
I agree that big limit is a good chance to find good student, but giving task that is practically impossible is not the same.
Long long time ago, the limit of problems wasn't big as present... but nowadays the limit is bigger, bigger after each year. But I think that a 9-grade student doesn't think about Miller-Rabin or some complex algorithms. Maybe a big limit is a good chance to find good student?
this problem is not hard , just u r stupid