A div2. Искомая строка — та, на которой звездочка встретилась ровно один раз, искомый столбец — тот, где звездочка встретилась только однажды. Перебрав все строки/столбцы и проверив количество звездочек в них, получаем ответ.
Авторы: MikeMirzayanov, Gerald .
B div2. Наивное решение за O(n3) (перебор всех троек с последующей проверкой) не укладывается по времени.
Заметим, что по двум точкам из тройки (скажем, это точки A и C) можно однозначно установить предполагаемое положение точки B. То есть достаточно перебора всех пар точек с последующий проверкой середины отрезка, их соединяющего.
Прибавим ко всем координатам точек 1000 (понятно, что ответ от этого не изменится) и отметим эти точки в двумерном массиве флагов размера 2001х2001. Теперь мы можем проверить есть ли в данной позиции точка или нет за O(1).
Объединим две последние идеи и получим верное решение за O(n2).
Авторы: MikeMirzayanov, Gerald
A div1. C div2. В данной задаче предполагалось жадное решение.
Зафиксируем две планеты: на планете i мы будем покупать товары, на планете j — продавать. Тогда прибыль с товара типа k будет равна b_jk-a_ik. Поскольку каждый товар занимает единицу места, нам выгоднее всего закупать для перепродажи товары в порядке уменьшения прибыли.
Отсюда сразу вытекает решение: перебираем все пары планет, для каждой пары сортируем товары в порядке уменьшения прибыли, после чего жадно закупаем самые прибыльные товары пока хватает места в трюме. Из всех пар планет выбираем ту, где суммарной получилось как можно больше.
Автор: Ripatti
B div1. D div2. Заметим, что операция split — это ничто иное, как циклических сдвигов строки. Мы можем переходить от любого циклического сдвига к любому другому кроме текущего.
Назовем циклический сдвиг хорошим, если он равен конечной строке. Все остальные сдвиги назовем плохими. Пусть у нас A хороших сдвигов и B плохих (проверить все сдвига на "хорошесть" можно в лоб за O(|w|2).
Обозначим за dpA[n] — количество способов получить хороший сдвиг за n split-ов, за dpB[n] — количество способов получить плохих сдвигов за n split-ов.
В начале либо dpA[0]=1, dpB[0]=0, либо dpA[0]=0, dpB[0]=1 в зависимости от того, хороший сдвиг начальной строка (= совпадает ли с конечной) или нет. Далее переходы легко выводятся:
dpA[n] = dpA[n-1] * (A-1) + dpB[n-1] * A
dpB[n] = dpA[n-1] * B + dpB[n-1] * (B-1)
Посчитаем все для n<=k, ответом будет dpA[k]. Итого решение за O(|w|2 + k).
Также, в этой задаче есть решение за 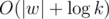 .
.
Автор: havaliza
C div1. E div2. У второго игрока есть довольно очевидная стратегия, позволяющая задержать фишку с начальными координатами (X, Y) в одной из 4х полуплоскостей — x ≤ X + 2, x ≥ X - 2, y ≤ Y + 2 и y ≥ Y - 2. Причем какая это будет плоскость — решать второму игроку.
Таким образом, если max(|x1 - x2|, |y1 - y2|) > 4, выигрывает второй игрок — он просто задерживает фишки в двух не пересекающихся полуплоскостях.
Оставшиеся случаи max(|x1 - x2|, |y1 - y2|) ≤ 4 предполагалось добивать перебором (возможно, с отсечениями). Понятно, что первому игроку ходить так, чтобы фишки "расходились" не выгодно, поэтому пространство перебора ограничивается квадратом 5 × 5. Если перебор не укладывается в 2 сек, можно сделать precalculation. Еще можно было написать дп на масках.
Кроме того, здесь можно было вывести формулу вручную. Однако тут много сложных для разбора случаев и легко ошибиться.
Автор: Ripatti
D div1. Заведем динамику dp[pre][len], в которой будем хранить наименьшую длину префикса гиперстроки, которая имеет с префиксом длины pre строки s наибольшую общую подпоследовательность длины len.
Тогда несложно получить формулы перехода:
dp[pre][len] = min(dp[pre - 1][len], наименьшая позиция буквы s[pre] в t правее dp[pre - 1][len - 1]).
Чтобы получать значения второго значения внутри минимума в вышеупомянутой формуле за O(1), нужно завести еще несколько динамик:
dp1 — для каждой базовой строки, позиции в ней и буквы посчитать самую левую позицию данной буквы правее данной позиции;
dp2 — для каждого элемента массива базовых строк (в гиперстроке) и буквы посчитать самую левую базовую строку, содержащую данную букву, правее данной базовой строки.
Итого решение за 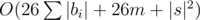 .
.
Автор: havaliza.
E div1. Сначала попробуем решить такую задачу: в деревы вебрано k вершин, нужно найти сумму ребер "натянутого" на них поддерева за 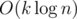 .
.
Упорядочим все k вершин в порядке обхода dfs — v1, v2, ... , vk. Рассмотрим пути v1-v2, v2-v3, ... , v(k-1)-vk и vk-v1. Нетрудно заметить, что они покрывают нужное нам поддерево, причем каждое ребро покрыто ровно два раза. Теперь, чтобы найти сумму ребер надо просто посчитать сумму всех путей (при помощи LCA это можно сделать как раз за 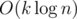 ), а потом просто поделить на 2.
), а потом просто поделить на 2.
Чтобы решить первоначальную задачу, нужно поддерживать множество активных вершин в упорядоченном состоянии (например, использую std::set) и сумму всех путей между последовательными вершинами. Теперь запросы на добавление и удаление вершин можно обработать за 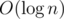 , после чего обновить текущую сумму пересчитав 3 пути — тоже за
, после чего обновить текущую сумму пересчитав 3 пути — тоже за 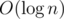 .
.
Итого имеем решение за 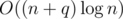 .
.
Автор: Ripatti.











А можно вот это место доказать более-менее строго, пожалуйста?
Если, например, одна левая из фишек ходит налево, то второй игрок теперь каждым ходом будет клеить клетку справа от этой фишки, если она сходила. Лучше первому игроку от этого точно не станет
(для случая (4,3) это точно правильно, а остальные случаи вроде бы на бумажке элементарно считаются)
Почему же не станет? Например, площадь незаклееных клёток увеличивается. С другой стороны, понятно, что за 5x5 мы никогда не выйдем (иначе применим соображение о полуплоскостях), поэтому перебор всё равно можно сделать.
Кто ещё решал B div 1 с ограничениями K <= 10^9? :)
Макс ты матрицу в степень возводил?
Ну да, а перед этим долго и упорно искал Формулу :)
Вот мне всегда было не понятно как авторам приходят в голову задачи наподобие С и самое главное ЗАЧЕМ они дают их на контест? Вообще контест сильно не понравился. Скорее всего из-за задач А и С после которых мозг вообще перестал работать. Задача А: про какие кредиты рассказывалось в условии, что за названия планет, почему они все различны, почему ограничения на n — 10 а не 100. Задача С просто бред. B и D клевые. Е не читал.
For problem D (div 2) the formula is slightly incorrect. Correction:
Yes, you're right.
Thank you, fixed
In div2 E. Why does the second win when the input is "5 5 1 1 5 4"
Brute force proves it
Did you write the program using brute force and find the regularity before you submit the problem?
Yes I am. But I've got Wrong answer on test 9 and then write brute force.
Первую задачу надо решать так:
На самом деле, первое решение, которое пришло мне в голову, такое же. Но словами его объяснять дольше, поэтому...
Лентяй я короче.
For div 1 B, I want to know that what are values A and B in the recurrence relations? Also I would like to find some AC submissions to this problem.
For Div1E I have an alternative solution which focuses on binary searching the LCA of a point and a set of points as I didn't noticed that I can double count all necessary path by sorting dfs visiting time.
Code: http://codeforces.me/contest/176/submission/20437271
(Now reviewing the code, the part of getLCA and sparse table is not required for finding LCA between a point and a set of points)
The current length of all necessary path is always updated.
Pre-processing:
dfs for finding the visiting time and ending time of each vertex. O(N)
Pre-calculate the binary exponential distance from each vertex to the 2^N parent. O(NlogN)
The current length of all necessary path is always kept
Keep a segment tree to check if there are any restored village in a sub-tree in O(logN) time, we will need it for the binary searches for the queries.
How to handle queries:
'+': Find two poitns: 1. the LCA of the village being restored with any other already restored villages, 2. the LCA of the new set of points. Update the LCA of all villages if necessary. This can be done in O(logN * logN) time.
'-': Find two points: 1. the LCA of the remaining set, 2. the LCA of the village being destroyed with any other villages that are still available. Update the LCA of all villages if necessary. This can be done in O(logN * logN) time.
Remember to handle cases where the restored villages set size if smaller than 2.
'?': Just return the length value, this can be done in O(1) time.
Total time complexity: O(NlogN + qlogN * logN), which is slightly worse than the intended solution but it still fits in the TL very easily.
One question... You say that there is O(|w|+log k) solution on B div1. D div2., but what is the solution? Please explain.
O(|w| + logk) solution for 176B - Word Cut (Div 1 B) 96438522