Hi !
Today while solving 356D - Монеты и мешочки I needed a function for bitset in order see what is the first set bit.I asked M.Mahdi and he told me about bs._Find_first(). for example:
bitset<17>BS;
BS[1] = BS[7] = 1;
cout<<BS._Find_first()<<endl; // prints 1
After more research , we found bs._Find_next(idx). This function returns first set bit after index idx.for example:
bitset<17>BS;
BS[1] = BS[7] = 1;
cout<<BS._Find_next(1)<<','<<BS._Find_next(3)<<endl; // prints 7,7
So this code will print all of the set bits of BS:
for(int i=BS._Find_first();i< BS.size();i = BS._Find_next(i))
cout<<i<<endl;
Note that there isn't any set bit after idx, BS._Find_next(idx) will return BS.size(); same as calling BS._Find_first() when bitset is clear;
UPD One question, bitset is 32 or 64 times faster than bool array?











Really nice, thanks! I just used something like this:
But your code is much better. Unfortunately it works only with GNU C++ compiler.
Does anybody know how to find lower bit index with O(1) for
uint32_toruint64_t?UPD It's easy if divide 32-bits number into 4 parts and use precalc.
__builtin_ctzand__builtin_ctzllcount amount of trailing zeros (or lowest set bit, which is the same) inint / unsigned intandlong long / unsigned long longintegers respectively (but for some reason, when argument is zero their return value is undefined). They are claimed to be O(1) and actually work rather fast (even precalc is not much faster then them, if faster at all), unlike__builtin_popcount, which is slightly slower than accurate handwrittenGreat! One more advantage to use GNU C++ compiler :)
Is there any documentation for this
_Find_next? What if I wanted to know the position of MSB in bitset? (without converting to string and then reversing it)What it MSB?
What is the time required for
_Find_first? Is it O(n) or O(1) or something like O(n / 32) ?O(n / 32).
Generally speaking Find_first uses 64 bit register. But speed will be near the same with 32 bit. So writing speed in big O/theta notation in this case is not quite right.
Yes, you're right, but using this notation is popular.
You're right and wrong at the same time. In more theoretical setting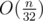 is just a shorthand for
is just a shorthand for 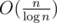 because that's what we get in most popular model of computation we use everyday where we are allowed to perform constant time operations on integers of size (==length of binary representation) up to logarithm of memory size. You wouldn't want adding two integers to take
because that's what we get in most popular model of computation we use everyday where we are allowed to perform constant time operations on integers of size (==length of binary representation) up to logarithm of memory size. You wouldn't want adding two integers to take  time, right?
time, right?
In more practical setting, we can express it as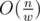 where w is a word size of system we are working on. But maybe in a parallel universe there are computers with word sizes of 1048576 :)? It shouldn't be simplified to O(n), since that w is clearly a variable, right? Fact that in all computers we have w is either 32 or 64 is another matter.
where w is a word size of system we are working on. But maybe in a parallel universe there are computers with word sizes of 1048576 :)? It shouldn't be simplified to O(n), since that w is clearly a variable, right? Fact that in all computers we have w is either 32 or 64 is another matter.
By the way, note the bridge between theoretical and practical setting — why is w 32 on older computer and 64 on newer ones? Because that is how many we need in order to address memory we want (lowest power of two to be more precise), so in fact w is really a logarithm of memory size we have access to.
I know i will get minuses again but i don't care. Even if ur a Legend you didn't right. In this case it doesn't matter what the word size of our computational model. Let w is computer word size and it is constant for computer. O(n/w) = O(n) and not equal to n/log n. Word will be the same and will be constant for computer it didn't depend on n.
In practice O can be used as a coefficient when we want to know how slow will be our algo if we multiply input by coefficient n. Let s is input data size and T(s) is execution time. And now we know T(s) for some s (is big). Now lets multiply s by n so T(s*n) = T(s)*O(n) this is how O notation works.
P.S. We didn't say about adding integers it is a bitset. So all i am saying above is about bitset operation. When we say about arithmetic on integers i will agree with you.
But as Swistakk wrote, theoretically w is not a constant. You may assume that your algo can be run on different machines with different architectures.
Formally speaking about math, with O notation for algorithm we estimate not an execution time for fixed computer, but the number of primitive operations, which will be different for machines with different w.
Formally speaking about practice, O(n/32) algorithms are usually much faster than O(n), so we write O(n) and O(n/32) to separate them.
w is not depend on n so O(n/log n) is not correct notation in any computation model (or any other sense) and is not the same O(n/w).
well, it kinda isn't and kinda is because in RAM-model you can do in O(1) operations on words you use to access memory. And you have n ≤ M ≤ 2w because if n > M you can't get such input and if M > 2w you can't access all of your memory. So you have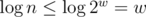
Ahh i see Legends and Grandmasters are joking me. Ok :). Let's continue. Memory size is not always lower than 2^w. See x86 XMS and EMS specifications.
We are speaking about models, not real PCs. On real PCs everything is O(1).
With all respect to Swistakk, MrDindows and riadwaw but RAM-machine computational model has unlimited input and output it has limited number of Registers and it is not the same. for example .... So i still think you are wrong. You can not limit n with 2^w.
P.S. For limited in/out you will always have complexity like in "real PCs everything is O(1)" (c) riadwaw
"Because the model assumes that the word size matches the problem size, that is, for a problem of size n,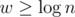 "
"
Quoted From This Wikipedia Article
I think this is the best blog for this kind of questions.
First question was already asked, how to find most significant bit in the bitset?
Second question, is there any way for easy manipulation with ranges in bitset — something like set all values in range (l, r) or flip all values in range (l, r)?
All this things can be done easy with own implementation of bitset, but is there any way to do this with std: : bitset.
bitset supports bitwise operators http://www.cplusplus.com/reference/bitset/bitset/operators/
so you can prepare a "mask bitset" (i.e. 000...001111...111000..000) and use it.
But it will work in O(n), not in O(r-l) as it could
It is good thing, you wrote this code! Now I can ask one more questions :)
What is complexity of creating one bitset of size n? Is it O(n), or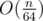 ? I do not see reason why it would be O(n), but from other side I know it has some other constructors with binary strings, which must be O(n).
? I do not see reason why it would be O(n), but from other side I know it has some other constructors with binary strings, which must be O(n).
You can do reinterpret cast of std::bitset pointer to the int32* and work with it like with your own implementation of bitset. This is what I usually do when I need some specific function for the std::bitset, that it does not have.
Thanks, it is not bad option too!
I don't remember it in details, but bitset in fact has a function for k-th bit, however it is declared as private... I have no idea why would someone not expose such useful function to world and deem it as private, but #define private public is there to help you. It really works. You need to look up implementation and figure out by yourself how is it called, maybe do some other trick etc. However I have to admit I was convinced that what I mentioned is the simplest way of getting first alive bit which is a very usual concern. Good to know it is as simple as that.
Other undocumented member functions of
bitset<Number_of_Bits>:Any of these functions does the same as its equivalent
The only difference is that the
Uncheckedversion assumes thatbit_positionis between0andNumber_of_Bits-\1. Therefore, no range checking to validate its value is performed. This can speed up repetitive processing of large-size bitset objects when the function argument is guaranteed to be valid before calling any of the former functions.Note that these undocumented functions are
publicmembers of the class. Therefore, the#define private publictrick is not required to use any of them.I couldnt find this, could you provide more details on this ?
Me — not really, I never used it. Maybe tribute_to_Ukraine_2022 can?