Только что закончился Гран-При Башкортостана. Подскажите, как решать F,J,M?
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
4 дня
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
4 дня
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 26.11.2024 11:13:30 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










J — мы должны найти ситуацию "в одном множестве вес набрали, в другом нет" (запустим решение, симметрично свапнем входные данные, запустим еще раз). Пишем рюкзак "какой минимальный вес может быть во втором множестве, если в первом вес Х и рассмотрели Y предметов". Все веса, которые больше 1е6 — обозначаем как 1е6, ведь нам достаточно знать, что мы уже набрали "очень много". Получается миллион на 100. Для восстановления ответа храним еще предков.
M — будем хранить троичную маску, которая для каждого столбца знает, что там еще не было единичек/сейчас единички/уже были единички. Сделаем по этим маскам дп по рваному профилю (+ храним число единичек в текущей строке), и посчитаем сколько есть валидных конфигураций для Х строк, для которых первая строка Y. Дальше восстановление комбинаторного объекта по номеру — перебираем маску в первой строке, начиная с самой маленькой в лекс. порядке, подобрав ее — перебираем во второй, и так далее.
Вопрос по K — как-то можно доказать, что из-за дополнительных ограничений на крутость данных (нету пересечений и коллинеарности, координаты маленькие) куб на самом деле не куб, или же просто тесты отстой? Наивное решение "пересекать все со всем", которое как бы куб, работает за секунду.
В K мои сокомандники сдали решение за O(n2logn) так, что куб наверное не предполагался.
Я полконтеста пытался подобрать тест против куба — не получилось :( Возможно даже, что его и нет. Авторское решение работает за
Как решать-то за ?
?
Переберем точку A. Делаем для нее сканирующую прямую по углу. Теперь, чтобы проверить подходит ли нам отрезок AB, достаточно только проверить пересечение этого отрезка с самым "близким" к A. Для этого когда двигаем прямую, будем складывать отрезки в Set с компоратором, схожий на тот, который описан на http://e-maxx.ru/algo/intersecting_segments
А как решать хоть за сколько-то?
Мы придумывали "найти все рёбра, которые можно провести, за O(n2logn), а потом построить на них миностов".
Как доказать, что существует миностов без пересекающихся рёбер?
Или у вас какое-то другое решение?
Мы так и делали. Формально доказывать не умеем, но мы исходили из минимизации ответа: если в ответе есть пара пересекающихся, то его можно улучшить.
Почему? Вдруг рёбра, на которые мы заменяем, с чем-то пересекаются?
Кажется, что можно так: давай у пересекающихся ребер сменим, что с чем соединено, но оставим отрезки с изломом (картинка не изменится, пересечение заменится касанием). Затем будем плавно стягивать их в прямую линию, тогда мы остановимся либо когда это превратится в отрезок, либо мы "натянем" наш отрезок на какие-то другие исходные точки, тогда его можно разбить на несколько отрезков без изломов.
Круто, спасибо!
Ну нужно доказать, что если у выпуклого четырехугольника одна диагональ строго меньше всех сторон, то вторая диагональ больше первой. Интуитивно, это очевидно, строго — надо посидеть с бумажкой.
по K — да, тесты оказались отстоем, мне стыдно. Сейчас сломал некоторые кубические решения.
Все-таки смогли завалить решение за куб. Возможно этот тест появится в дорешке.
Как в J хранить предков, они же в 64MB памяти не влезают?
vector<bool>В J можно не хранить предков, а сразу поддерживать ответ, благо множество взятых "предметов" помещается в двух лонгах
Как искать кратчайший цикл, содержащий данную вершину (задача F)?
Вы же её сдали? Из каждой вершины запускаем Дейкстру за квадрат. Смотрим те рёбра которые ведут в разные поддеревья корня дерева кратчайших путей или в корень, и ими апдейтим ответ.
Это слишком клевое решение, чтобы мы его могли придумать :) у нас решение за n3.5, мы бьем вершины на блоки по корню, после чего с помощью некоторой модификации алгоритма Флойда получаем для каждой вершины v матрицу кратчайших расстояний для графа без вершины v, а по ней восстановить ответ легко.
Можно делать то же самое, только пользуясь структурой дерева отрезков, тогда будет n^3 logn.
Да, я подумал об этом, но решил, что корень от логарифма не сильно отличается для трехсот, да и константа получше будет. В любом случае, то, что сказал Эдик выше, гораздо эффективнее.
Просто некоторые авторы очень любят давать баяны. click
Ну, в оправдание авторов можно сказать хотя бы то, что описанное решение в чистом виде не пройдет. =)
У нас вероятностное решение. Выберем вершину, будем временно удалять ребра из нее с вероятностью 1/2 и пускать Дейкстру. После этого пробуем идти по дереву кратчайших путей и возвращаться по одному из удаленных ребер. Каждая итерация находит правильный ответ с вероятностью как минимум 1/2.
Ага, у нас то же самое (придумал ilyakor). Мы смотрели на это немного по-другому: раздвоим вершину, и все ребра отправим в случайную из двух копий, потом найдём кратчайший путь между копиями.
Но это легко доделывается до детерминированного (как у нас) — будем пускать ребра в вершины с 0 в i бите в одну из раздвоенных, а с 1 в другую. За логарифм раз мы все пары в разные хоть раз пустим
Кстати да, отлично :)
Как преодолеть ML в E?
А как получить? Можете хотя бы вкратце описать решение?
Наше решение, видимо, чересчур сложное, но использует лишь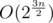 памяти (если точно, то 214·26 long long-ов), решим сперва для полностью пустой полоски:
памяти (если точно, то 214·26 long long-ов), решим сперва для полностью пустой полоски:
dp[mask][mask_good]— количество способов получить из уже поставленной позиции корректную, гдеmask— маска уже занятых нечётных позиций,mask_good— маска использованных хороших чисел. Когда мы ставим очередное число, оно минимальное среди уже поставленных. Это значит, что содержимое чётной позиции можно определять, когда оба соседа уже поставлены и оно будет ограничено половиной только что поставленного соседа. Соответственно, когда ставим большое число на какую-то нечётную позицию, смотрим, какие из соседних чётных позиций стали иметь двух занятых соседей и перебираем, что мы на эти позиции поставим — плохое число (неважно какое, они (пока) все для нас одинаковы, а оставшееся их количество изmaskиmask_goodопределяется однозначно) или одно из свободных хороших.Есть очень простое решение за 2k
Чуть подробнее объясните, пожалуйста.
Мы ставим числа от k до 1 на нечетные позиции. Состояние динамики — собственно занятые нечетные позициии. Более подробно можно будет в коде посмотреть когда у сеня руки дойдут его впушить
Вот код
Как решать I?
Если мы узнаем число, загаданное сервером — сможем легко выиграть.
Чтобы узнать число, загаданное сервером, достаточно сыграть около 40 раз — мы получим последовательность проигрышей и выигрышей, которая однозначно задает число (конечно, в связи со спецификой генератора чисел).
У меня получилось, что не однозначно. Около 300 пар чисел не различаются, но видимо они никогда не различаются дальше. Во всяком случае, их не надо различать, чтобы найти момент, когда постаивть много.
Довольно странно — у нас
assertна этот факт в решении, причем с 32-мя шагами он падал.Хм. Ну, у меня почему-то различных значений масок получалось меньше. Проверял также. В целом, не так важно. Важно, что по первым 35 можно предсказать следующие 25
А у кого-нибудь есть решение задачи G с доказательством (хотя бы корректности, если не времени). Я написал что-то, оно прошло тесты, но почему не бывает ситуации, когда решение можно однозначно вывести, а мое решение не сможет, я не понимаю.
А в чем именно трудность? У нас есть некоторый набор условий, и мы динамикой по профилю (профиль — состояние закрытых клеток, у которой мы уже рассмотрели хотя бы одного соседа-числа, но не рассмотрели всех) проверяем, может ли каждая из неизвестных клеток быть миной. Если каждая может — значит безопасного хода нет, если какая-то не может — ходим туда.
А хоть какое-нибудь понимание, почему это работает быстро, есть?
Ну идея есть, хотя формального доказательства нет. Видимо верно что-то в стиле того, что множество открытых клеток + известных мин всегда 4-связно, поэтому его граница это один контур, и если мы будем обходить его по порядку, то ни в какой момент клеток в профиле не будет больше 6 или около того.
К сожалению граница это дерево. Например, могут первым же ходом открыть букву Ш например.
Who can explain problem D ? We solved it with binary_search, and for any step of binary_search we just check if it fits the given size or not, but we get Wrong Answer on test 2.
Binary search do not work in this problem. Say for 1,1,100,100 and w=103 you can choose l=2, but for l=3 it won't fit
Thank a lot bro
Where can I find the problems?
https://www.dropbox.com/s/gulwb6ec5drwftx/problems-e-010342.pdf?dl=0
Div. 2. How to solve O, Q? We haven't understand problem statement of 'O' or it's test cases #1 and #2: input "1" and "2" haven't any neighbour digits. In 'Q' we substituted every longest possible jump from one dot (marsh in beginning of string) to another with a dot, and repeated until string become '.' (means 'OK'):
while( s/^ \. .{0,$j} \././x ){$count ++}(.{min,max}is greedy and tries to match as much as possible any chars, and if following dot\.mismatch then.{min,max}backtracks until\.match, otherwise substitution fails), but had WA #2.O can be solved in O(1) by precalculations (only 512 answers) or O(n) finding solution directly. cycling from 1 to 2500000 and count how much acceptable integer founded. In C++ checking int would look like this:
Q is simple DP with checking for traps. dp[i] = min {dp[i-j], ..., dp[i-1]}+1
Can somebody explain me problem N(div2)? I would like to see a solution to this problem with proof? We computed the sum of an arithmetic progression and compared it with given x. And we considered that x must be not greater than sum. But we got WA2.
Notice that a + b and a - b have the same parity. Let S = 1 + 2 + .. + n, then x and S should give the same remainder mod 2. And x must be not greater that n, because |a - b| ≤ max(a, b) for any positive integers a, b.
тогда непонятно, что может быть в тесте 2. потому что по сути, из вашего доказательства следует, что наше решение должно быть правильным. Upd. я понял ошибку. спасибо за ответ