Mo's Algorithm on Trees [Tutorial]

№	Пользователь	Рейтинг
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Introduction

Mo's Algorithm has become pretty popular in the past few years and is now considered as a pretty standard technique in the world of Competitive Programming. This blog will describe a method to generalize Mo's algorithm to maintain information about paths between nodes in a tree.

Prerequisites

Mo's Algorithm — If you do not know this yet, read this amazing article before continuing with this blog.

Preorder Traversal or DFS Order of the Tree.

Problem 1 — Handling Subtree Queries

Consider the following problem. You will be given a rooted Tree T of N nodes where each node is associated with a value A[node]. You need to handle Q queries, each comprising one integer u. In each query you must report the number of distinct values in the subtree rooted at u. In other words, if you store all the values in the subtree rooted at u in a set, what would be the size of this set?

Constraints

1 ≤ N, Q ≤ 10⁵

1 ≤ A[node] ≤ 10⁹

Solution(s)

Seems pretty simple, doesn't it? One easy way to solve this is to flatten the tree into an array by doing a Preorder traversal and then implement Mo's Algorithm. Maintain a lookup table which maintains the frequency of each value in the current window. By maintaining this, the answer can be updated easily. The complexity of this algorithm would be 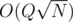$\text{[math]}$

Note that you can also solve this in 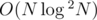$\text{[math]}$ by maintaining a set in each node and merging the smaller set into the larger ones.

Problem 2 — Handling Path Queries

Now let's modify Problem 1 a little. Instead of computing the number of distinct values in a subtree, compute the number of distinct values in the unique path from u to v. I recommend you to pause here and try solving the problem for a while. The constraints of this problem are the same as Problem 1.

The Issue

An important reason why Problem (1) worked beautifully was because the dfs-order traversal made it possible to represent any subtree as a contiguous range in an array. Thus the problem was reduced to "finding number of distinct values in a subarray [L, R] of A[]. Note that it is not possible to do so for path queries, as nodes which are O(N) distance apart in the tree might be O(1) distance apart in the flattened tree (represented by Array A[]). So doing a normal dfs-order would not work out.

Observation(s)

Let a node u have k children. Let us number them as v₁,v₂...v_k. Let S(u) denote the subtree rooted at u.

Let us assume that dfs() will visit u's children in the order v₁,v₂...v_k. Let x be any node in S(v_i) and y be any node in S(v_j) and let i < j. Notice that dfs(y) will be called only after dfs(x) has been completed and S(x) has been explored. Thus, before we call dfs(y), we would have entered and exited S(x). We will exploit this seemingly obvious property of dfs() to modify our existing algorithm and try to represent each query as a contiguous range in a flattened array.

Modified DFS-Order

Let us modify the dfs order as follows. For each node u, maintain the Start and End time of S(u). Let's call them ST(u) and EN(u). The only change you need to make is that you must increment the global timekeeping variable even when you finish traversing some subtree (EN(u) = ++cur). In short, we will maintain 2 values for each node u. One will denote the time when you entered S(u) and the other would denote the time when you exited S(u). Consider the tree in the picture. Given below are the ST() and EN() values of the nodes.

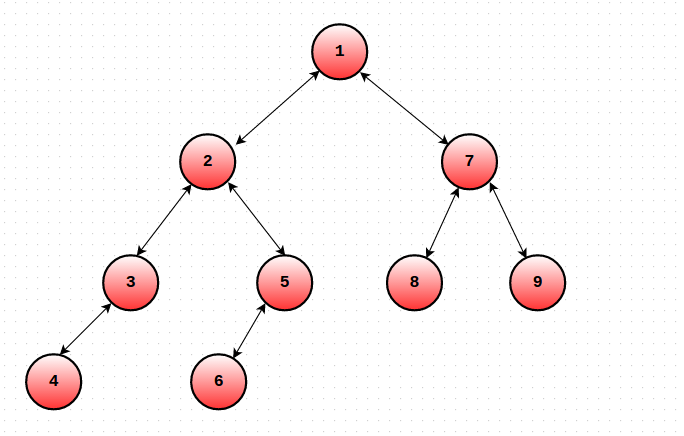
ST(1) = 1 EN(1) = 18

ST(2) = 2 EN(2) = 11

ST(3) = 3 EN(3) = 6

ST(4) = 4 EN(4) = 5

ST(5) = 7 EN(5) = 10

ST(6) = 8 EN(6) = 9

ST(7) = 12 EN(7) = 17

ST(8) = 13 EN(8) = 14

ST(9) = 15 EN(9) = 16

A[] = {1, 2, 3, 4, 4, 3, 5, 6, 6, 5, 2, 7, 8, 8, 9, 9, 7, 1}

The Algorithm

Now that we're equipped with the necessary weapons, let's understand how to process the queries.

Let a query be (u, v). We will try to map each query to a range in the flattened array. Let ST(u) ≤ ST(v) where ST(u) denotes visit time of node u in T. Let P = LCA(u, v) denote the lowest common ancestor of nodes u and v. There are 2 possible cases:

Case 1: P = u

In this case, our query range would be [ST(u), ST(v)]. Why will this work?

Consider any node x that does not lie in the (u, v) path.
Notice that x occurs twice or zero times in our specified query range.
Therefore, the nodes which occur exactly once in this range are precisely those that are on the (u, v) path! (Try to convince yourself of why this is true : It's all because of dfs() properties.)

This forms the crux of our algorithm. While implementing Mo's, our add/remove function needs to check the number of times a particular node appears in a range. If it occurs twice (or zero times), then we don't take it's value into account! This can be easily implemented while moving the left and right pointers.

Case 2: P ≠ u

In this case, our query range would be [EN(u), ST(v)] + [ST(P), ST(P)].

The same logic as Case 1 applies here as well. The only difference is that we need to consider the value of P i.e the LCA separately, as it would not be counted in the query range.

This same problem is available on SPOJ.

If you aren't sure about some elements of this algorithm, take a look at this neat code.

Conclusion

We have effectively managed to reduce problem (2) to number of distinct values in a subarray by doing some careful bookkeeping. Now we can solve the problem in 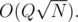$\text{[math]}$ This modified DFS order works brilliantly to handle any type path queries and works well with Mo's algo. We can use a similar approach to solve many types of path query problems.

For example, consider the question of finding number of inversions in a (u, v) path in a Tree T, where each node has a value associated with it. This can now be solved in 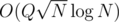$\text{[math]}$ by using the above technique and maintaining a BIT or Segment Tree.

This is my first blog and I apologize for any mistakes that I may have made. I would like to thank sidhant for helping me understand this technique.

Sample Problems

1) Count on a Tree II
2) Frank Sinatra — Problem F
3) Vasya and Little Bear

Thanks a lot for reading!

Original Post
Related Blog

#include "bits/stdc++.h" using namespace std; typedef pair < int, int > pi; typedef vector < int > vi; typedef vector < pi > vpi; const int MAXN = 1e5 + 10; const int SQRT = 320; const int LOGN = 20; int A[2*MAXN]; pi B[MAXN]; int V[MAXN], C[MAXN]; int D[SQRT + 10][SQRT + 10], S[SQRT + 10]; int P[MAXN]; vpi G[MAXN]; int W[MAXN], R[MAXN]; struct query { int x; int y; int ind; }; query Q[MAXN]; bool comp(query a, query b) { if (int(a.x/SQRT) != int(b.x/SQRT)) return (int(a.x/SQRT) < int(b.x/SQRT)); return a.y < b.y; } int cont = 0; void dfs(int x, int p) { V[x] = 1; P[x] = p; A[cont] = x; B[x].first = cont; cont++; for (int i = 0; i < G[x].size(); ++i) { int y = G[x][i].first; int k = G[x][i].second; if (!V[y]) { C[y] = k; dfs(y, p + 1); } } A[cont] = x; B[x].second = cont; cont++; } void add(int x) { int k = C[A[x]]; if (k > MAXN) return; if (!W[A[x]]) { if (D[k/SQRT][k%SQRT] == 0) ++S[k/SQRT]; ++D[k/SQRT][k%SQRT]; ++W[A[x]]; } else { if (D[k/SQRT][k%SQRT] == 1) --S[k/SQRT]; --D[k/SQRT][k%SQRT]; --W[A[x]]; } } int main() { ios_base::sync_with_stdio(false); cin.tie(0); int n, m; cin >> n >> m; for (int i = 1; i < n; ++i) { int x, y, val; cin >> x >> y >> val; --x; --y; G[x].push_back(pi(y, val)); G[y].push_back(pi(x, val)); } dfs(0, 0); C[0] = MAXN + 1; for (int i = 0; i < m; ++i) { int x, y; cin >> x >> y; --x; --y; if (B[x].first > B[y].first) swap(x, y); if (B[x].second > B[y].second) { Q[i].x = B[x].first + 1; Q[i].y = B[y].first; } else { Q[i].x = B[x].second; Q[i].y = B[y].first; } Q[i].ind = i; } sort(Q, Q + m, comp); int a = 0; int b = -1; for (int i = 0; i < m; ++i) { while (b < Q[i].y) { ++b; add(b); } while (a > Q[i].x) { --a; add(a); } while (b > Q[i].y) { add(b); --b; } while (a < Q[i].x) { add(a); ++a; } for (int w = 0; w < SQRT; ++w) { if (S[w] < SQRT) { for (int j = 0; j < SQRT; ++j) { if (D[w][j] == 0) { R[Q[i].ind] = w*SQRT + j; break; } } break; } } } for (int i = 0; i < m; ++i) cout << R[i] << endl; }

if (B[x].first > B[y].first) swap(x, y); if (B[x].second > B[y].second) { Q[i].x = B[x].first + 1; Q[i].y = B[y].first; } else { Q[i].x = B[x].second; Q[i].y = B[y].first; } Q[i].ind = i;

Комментарии (136)

Показать архивные | Написать комментарий?

meintoo

9 лет назад, # |

← Rev. 2 →

In this case, our query range would be [EN(u), ST(v)] + [ST(P), ST(P)].
Shouldn't it be [EN(u), ST(v)] + [ST(P), ST(U)] or am I missing something ?

→ Ответить

animeshf

9 лет назад, # ^ |

Nope, it will be [ST(P), ST(P)].

Consider the path from 3 to 5. In this case, P = 2

EN(3) = 6 and ST(5) = 7, so we consider the range [6, 7] in A[] corresponding to the nodes [3, 5] giving us the values of nodes 3 and 5.

Our query range does not consider the value of the lca as ST(P) < EN(u) < ST(v) < EN(P). Hence we must account for the value of P separately.

Ok !!!
Thanks
Nice article anyways

+13

Thank You :D

sampriti

+23

Thanks! That was a really nice tutorial!

Thanks a lot :)

brainstorm

Nice tutorial :)
can you give links to some more problems on which similar approach can be applied ?

sbansalcs

8 лет назад, # ^ |

http://codeforces.me/problemset/problem/375/D

This can be done with standard Mo's Algorithm, because the queries are on subtrees and not paths.

Oh sorry, I thought this guy was asking for any problems related to the algorithms described above.

hmrockstar

7 лет назад, # ^ |

but in each query, there is a new k. I wrote code for this problem, after whole implementation, i noticed that i missed the point that there is alway a new k for each query. Now i am not getting how can i solve this prob!

my code!

komendart

BTW, we can find number of distinct values in a subarray [l, r] of a offline in O((q+n)\log n).

Let's sort all queries by l_i.

d_i = 1 if i is the first occurence of a_i in a[l...n] otherwise d_i = 0.

So, query (l_i, r_i) is finding sum of d[l_i...r_i].

When we move from query with l_i to query with l_i + 1 we must update only one or zero elements of d_i. It can be done in $\text{[math]}$ if we precalculated for each i next occurence of a_i in array.

gongy

+10

If you maintain the tree persistently, you can have an online solution as well.

joker_in

-6

can you elaborate it . how to handle it online ? thanks in advance.

bhishma

I think this is related to a current running contest.

yes

SarvagyaAgarwal

which contest ?

codechef feburary long challenge

In curiosity i asked this question too early . sorry for that . you can answer it after contest is over

Yeah , 3 days early :P

FLYSKY

Contest has ended 3 months ago..

Can anyone please answer this question now ?

Can you please explain it how to do it online ?

-7

Create an array of next occurences and build a persistent segment tree on that . The key idea is that number of distinct values in [L,R] is number of values whose next occurence is > R .

bluemmb

Thanks, Is known who used this idea on trees first time ?

belltolls

It must have been known from before. But I guess this is the first proper tutorial/blog for it.

xrisk

Totally went over my head! Excellent blog!

R2__D2

If it goes over your head, How do you realize it's an excellent ?

svg_af

Thanks a lot you made my day !!

I've been obsessing about COT2 for almost two months without anything that comes to mind

if only i could upvote more than once

Thanks! I'm glad that you found it useful :)

rachitiitr

I implemented this algorithm on the COT2 problem on SPOJ(http://www.spoj.com/problems/COT2/). I am getting WA. Can someone help me identify the bug in my code? http://ideone.com/aLS5Yx

I found the mistake. Thanks for the nice tutorial.

What was the bug ?

Lol. Bro that was 7 months ago.

Can you share your corrected code ? Because I'm getting a WA too .

Sure. Link

vasandani68

Can u please explain ur add and del functions. How are u maintaining the result after ignoring all those indexes which have occured 2 times?

Recently I solved one question using Mo's algorithm, and I remembered about this comment here. I overwrote the solution on the same link. Here is the solution for COT2. I think its self-explanatory how it is working.

NiKS001

Can someone please provide the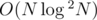 algorithm for Problem 1?

The best I could get is (N^2)*logN [as the sum of sizes of sets of each node is O(N^2) — Worst case linear graph with all values distinct]

← Rev. 4 →

Maintain a set of values for each node in the tree. Let set(u) be the set of all values in the subtree rooted at u. We want size(set(u)) for all u.

Let a node u have k children, v₁, v₂...v_k. Every time you want to merge set(u) with set(v_i), pop out the elements from the smaller set and insert them into the larger one. You can think of it like implementing union find, based on size.

Consider any arbitrary node value. Every time you remove it from a certain set and insert it into some other, the size of the merged set is atleast twice the size of the original.

Say you merge sets x and y. Assume size(x) ≤ size(y). Therefore, by the algorithm, you will push all the elements of x into y. Let xy be the merged set. size(xy) = size(x) + size(y). But size(y) ≥ size(x).

So size(xy) ≥ 2 * size(x).

Thus, each value will not move more than log n times. Since each move is done in O(logn), the total complexity for n values amounts to O(nlog² n)

Code

Awesome! Thanks for the great explanation and code!

I_love_Captain_America

← Rev. 3 →

I don't get the proof. Can you explain it a little more?

size(xy) ≥ 2 * size(x)

I think, size(xy) >= size(y), and size(xy) <= size(x) + size(y)

Thus, each value will not move more than log n times.

How?

EDIT I think I understood. For a particular value to be included the maximum number of times in a move operation from set(x) to set(xy) where size(x) <= size(y), this value must be moved for each of it's ancestor upto root. That is only possible if the height of the tree is at most log n.

But the size(xy) >= 2 * size(x) seems incorrect. I think you meant that the size of subtree of parent of x >= 2 * size(x).

iit2015023

We cannot use the size function of the set to compare the sizes of the set as it would otherwise lead to N^2 complexity.Am i right?

set.size() is O(1).

I thought it is O(n).Thanks for the info.

himanshujaju

Very neatly written tutorial. You make it seem amazingly easy!

mbrc

+11

Superb idea! :D

Thanks! :D

demon_cross

Nicely written!

Thanks a lot :D

naruto09

shouldn't it be end time of u to start time of v in case 1.If we start from start time of u then u will be included 2 times one for its start time and once for end time.Correct me if i am wrong..

Case 1 implies that u is an ancestor of v.
Therefore, we won't visit u twice in the range [ST(u), ST(v)] as EN(u) > ST(v).

baobab

Has anyone managed to get accepted on the SPOJ problem with a Java solution? I'm getting NZEC Runtime Error, but it looks like it's actually due to time limit exceeding.

Update 1: Added sample problems.

Absolut

For the "Frank Sinatra" problem. How could you find the less value not present in the path?

I realize that any value greather than the size of the tree wouldn't change the answer. So, if i have at most 1E5 different values I can build a BIT. pos[i] = 1 if value i is present in the path. Then I binary search the less value k wich sum[0...k] is less than k. That would be my answer. However the complexity is O(N*sqrt(N)*log(N)*log(N)) and I think is excesive.

The complexity wouldn't be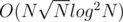 $\text{[math]}$ , it would be $\text{[math]}$ .
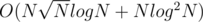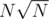The first term is because you update your bit atmost $\text{[math]}$ times and the second term is because you binary search once for each query.

Thanks, my mistake.

So, it is the best completely? Or there is another approach

You can solve the problem in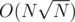 $\text{[math]}$ by doing square root decomposition on the values. Each update would be done in constant time and you will take additional 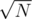$\text{[math]}$ time per query to find the block which has the smallest value.

_LNHTD_

5 лет назад, # ^ |

In your code, I saw this:

Can " if (B[x].second > B[y].second) " replace LCA(x, y) == x ?

I also want to ask does the O( N * sqrt(N) * log(N) + N * log (N) ) algorithm pass this problem ?

SProf

can it gives me tle,if i can't use weight compress?

If you do not compress weights, you'll need a map and that would add an additional log(n) factor. However, you might be able to squeeze your solution within the TL with an unordered_map.

meshanya

+39

BTW, there is a standard solution for the first problem (see this link in Russian). For each of the colors order all the vertices of this color according to the dfs traversal, let the vertices be labelled v₁, v₂, ..., v_k. Add +1 to each of these verticies, and add -1 to the LCAs of the neighboring vertices lca(v₁, v₂), lca(v₂, v₃), ..., lca(v_k - 1, v_k). If you sum up the values inside a subtree, you get the number of distinct elements in it.

Since the ordering can be done in O(n), and in theory you can answer lca queries for a static tree in O(1) with O(n) pre-processing, you have a linear solution (assuming 0 ≤ A[x] < N).

Thanks! This idea is pretty cool :)

-synx-

I understand the merging sets optimization!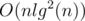
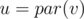
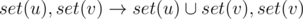
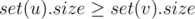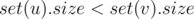Can you explain how we can utilize this in Problem 1 (unique elements in subtree) to achieve $\text{[math]}$ ?
As far as I see, lets say $\text{[math]}$
then we want, to change $\text{[math]}$
which can be done optimally when $\text{[math]}$ ,
how do you propose to do it for $\text{[math]}$ ?

howsiwei

Isn't the time complexity of Mo's algorithm O(N*sqrt(Q)) instead of O(Q*sqrt(N))?

The complexity of Mo's depends on the number of times we increment/decrement the curL, curR variables. This link explains the time complexity of Mo's algorithm.

If the size of each block is k, then the time complexity of moving the left pointer is O(Q*k) and the time complexity of moving the right pointer is O(N/k*N). The optimal value of k is N/sqrt(Q) which results in total time complexity O(N*sqrt(Q)).

That is true. However, in most cases upper bounds on Q and N are equal (or pretty close), so it doesn't make a difference.

aashishkr

I wrote the code for COT2 judge gives runtime error at 10th testcase pls help me i cant find the error thanks in advance

pls see my code

https://ideone.com/MG3XbK

Peregrine_Falcon

I think it's for the weight value. They haven't said anything about the limit. I compressed the weights.

8 лет назад, # |

+19

Awesome Tutorial!

Thank you!

alphaguy4

Can anyone explain how to linearize the tree .. (Not binary tree but any tree in general)

As in Problem 1..

Click

uttom

I got Runtime Error. Here is my code There is any wrong my crealting lca tabel or anything else. Thanks in advance.

ankeshgupta007

amazing tutorial!

stould

If the tree store the values on the edges, you could store these values on the children (going from the root), and change the Case 2 to:

if(P == u || P == v) check(P);
.... asnwer the query
if(P == u || P == v) check(P);

mochow

Why don't you write more tutorials?

COT2 code link doesnt work .

Updated.

Why does this get WA for COT2 :/ ?

ace_pocket

Could you explain your idea for the problem of finding number of inversions in a (u, v) path in a Tree T.

Just maintain a BIT during Mo's

Vicennial

If I flatten the above tree, my array would be:
8 3 1 6 4 7 10 14 13
Suppose I need to use Mo's algorithm for subtrees(assume I need to find sum of values of each subtree indicated by the query)
For a given query 'Vj' how would I find its end range index in the array?
Eg if given query is node '6', the starting range would be idx 3 and ending would be idx 5.

Store the starting and ending times for every node during your dfs .

Thanks, understood it after a bit of googling about discovery/begin/end times.

Tobby_And_Friends

For a problem like this: http://lightoj.com/volume_showproblem.php?problem=1348 where I need to return sum of all the nodes in a given path & update the value of a node, how should I approach using this technique of linearizing the tree? I mean since I need to ignore nodes which have occurrence of 2 so the range becomes discontinuous for a segment tree structure.

Boxer

I think you should use Heavy light decomposition(HLD).

https://wcipeg.com/wiki/Heavy-light_decomposition

aniervs

It can be done without HLD. Let be dp[u] the sum of values of path from root downto u. The sum of values on the path from u to v is dp[u]+dp[v]-2*dp[L]+val[L] where L is lca(u,v). When you change the value of a node u, you must change dp[v] for all v belonging to subtree of u. With an euler tour the subtree of a node becomes a continous subarray, so you can easily update it with a segment tree or similars.

arjun95

How can apply this method if weight is given on edges instead vertices

Root the tree arbitarily . Map the weight of edge (parent-child) to the child .

and what about the weight of root?

Are you saying that both edges and nodes have weights ?

no, i mean as you said map the weight of edge (parent-child) to the child but root has no parent so what value is map to the root of the tree?

nothing is mapped to the root . A tree has n — 1 edges which would be mapped to n — 1 vertices of the tree .

assign it an impossible value like -INFINITY. This means whenever you see this value, you know it's not allowed, and you ignore it.

hiddentesla

how to calculate LCA fast? i only know the O(n) algorithm...

CuSO45H2O

Consider on this case, if we select 3 and 8 on the tree given to explain the DFS-Order, the range[EN(u), ST(v)] contains the whole subtree S(5) which is not on our query path. Are we supposed to judge every node in the range or Am I missing something? Thx!

you only consider nodes which appear once in the range, so maintain a frequency count of the current nodes, if a node appears twice, remove it from the list of nodes

fane_faiz

Man, you nailed the use DFS. BTW thanx for the amazing article.

vatsal

"One easy way to solve this is to flatten the tree into an array by doing a Preorder traversal" Isn't Preorder traversal done on a binary tree? The given tree may not be a binary tree. Where am I going wrong?

By Preorder, I meant that we look at the value of v before looking at the value of all of its descendants.

i_love_emilia_clarke

How would we handle nodes which occurs two times because they were not in the required path ?In other words how would we remove their contribution ?

sanket407

keep separate counter for counting occurences of element in present range !!

while changing L and R,

if occurence of element becomes 1 from 2 then consider that element as ADDED

if occurences of element becomes 0 from 1 then consider that element REMOVED if occurences of element becomes 2 from 1 then consider that element REMOVED if occurences of element becomes 1 form 0 then consider that element ADDED

adamantium

7 лет назад, # |

Is the idea of converting a tree into a linear array is applicable on segment tree? If applicable then how to handle which node appear 2 times

Tutis

You cannot really do it. You should use heavy light decomposition.

griever

Please if anyone can explain the struct part in the code mentioned in the blog. Here's the code snippet

struct query
{
    int id,l,r,lc;
    bool operator < (const query& rhs)
    {
        return (BL[l] == BL[rhs.l]) ? (r<rhs.r) : (BL[l] < BL[rhs.l]);
    }
}Q[MAXM];

Complete Code Link

I am not able to understand the bool operator part.What is it doing and how?

Flyce

To sort queries we need to know how to compare them, it can be done by overloading operator < or making a bool function (comparator) which takes two queries and return true if first must be to the left of the second in sorted array.

Thank you for explaining :-)

It is sorting the l values according to the BLOCK value of l i.e. BL[l]. If both the values are same then it compares the one which has smaller r value just like in Standard Mo's algorithm. Am I interpreting it right?

Yeah, firstly we compare blocks of left edge and compare right edge if they are equal.

shbhm_5301

very nicely explained. thanks a lot animeshf this article is very helpful

xxxcxxx

Is the range went wrong. For example:

If we modify dfs-order then we will have : 1-2-3-4-5-6-7-8-9-10-11. We have a query count distinct number in unique path from 4 to 11. Then the answer contain S(5) — out of path from 4 to 11 ??

Am I missing something ?

phibrain

i think DFS-order will be 1-2-3-3-4-4-2-5-6-6-7-7-5-8-9-9-10-10-11-11-8-1, EN[4]=6, ST[11]=19, so the nodes which occur exactly once in this range are 4,2,8,11; then you have to consider also ST[1]=1 .In the end you have 4,2,8,11,1

fsociety00

Can anyone tell me how to solve Vasya and little Bear problem (3rd problem) ??

linus509

6 лет назад, # |

-8

What is the use of VAL[] in the ideone link provided ? I mean i understand the use of A[x] that stores the position of x in sorted weights..

chinmay0906

Nice tutorial!! A problem using this concept 852I - Dating.

5 лет назад, # |

In case any body isn't clear about how to transform the tree- I run a simple DFS, save them in an N+N sized array, by the order of starting & finishing time. Then ordered the queries offline by the given node's starting and ending time. Just run the query by MO's. I love this problem.

JacobianDet

Can someone explain that inversion count example in the tutorial as it's unclear to me? Also, can a problem link be given for that?

roll_no_1

[Deleted]

vasu2907

Thanks!! This blog was extremely helpful for me.

cicada2020

please explain the use of const int LN = 17 in your code

LanceTheDragonTrainer

← Rev. 6 →

You mean LN=19 rather? It seems to be used for setting the size of the first dimension of the sparse table. Because 2^19 is quite a huge value (> 500K). So the author probably doesn't need to worry about running out of bounds. You know that one dimension of the sparse table has to be log(N) where N is the size of the array you are computing over right? So LN must be stated such such that 2^LN > N.

AM_I_Learning

A problem in April LOng Appears om this concept : link is

FCTRE

Suri429

Thanks for the amazing tutorial !

Surender21

Great tutorial ! I wanted to know, if MOs can be applied, when edges are weighted and nodes don't have any value. In some of the cases, like sum of edges on path, I thought of distributing the weights of edges on the nodes , which are connected by the edge. So we can sum up the nodes + add an extra u,v and then dividing it by 2.

Is there a general way to approach such type of queries ? Thanks

RisingWizard

4 года назад, # |

I tried to solve the Problem 1 using Segment Tree but it is giving TLE Problem Link

I think merging two sets is taking linear time How do I optimize it?

_Bishop_

Nice algorithm and blog

Algo_Daddy

How to find the LCA of two nodes here.. is there any simpler way than doing binary lifting??

Rook_Lift

3 года назад, # |

where can i submit code for Frank Sinatra — Problem F ?

-is-this-fft-

3 года назад, # ^ |

+16

You can submit it in the gym contest it was taken from.

Si_jo

2 года назад, # ^ |

Did you get AC in it ? If yes, can you please share your code ?

2 года назад, # |

How to solve Vasya and little bear ?

Sefineh_Tesfa

20 месяцев назад, # |

Thanks for sharing. It is amazing! - In case I: It says [ST[u], ST[v]], but couldn't it be [EN[u], ST[v]]? In Problem 2 — Handling Path Queries, A[] = {1, 2, 3, 4, 4, 3, 5, 6, 6, 5, 2, 7, 8, 8, 9, 9, 7, 1} Let's says the query is from node 4 to node 6. So, couldn't the query looks like [EN[4], ST[6]]? Sorry, I am a little bit confused.

lis05

20 месяцев назад, # ^ |

In case 1, if $$$u$$$ is the ancestor then range $$$EN[u],ST[v]$$$ won't work because when you exit node $$$u$$$ you won't be able to reach node $$$v$$$ which is below $$$u$$$

IbrahimHiarea

18 месяцев назад, # |

Nice blog

script.kidd

10 месяцев назад, # |

I believe the range

$$${[ST(u)+1, EN(v)-1] \cup [ST(P), ST(P)]}$$$

works regardless of whether $$$P=u$$$ holds, assuming $$$ST(u) \le ST(v)$$$.

Worked example: 245030038