Доброго времени суток! Программисты, которые умеют писать Splay tree — подскажите, по каким статьям/лекциям учились его писать ? Ну и, если можно, подкиньте задач, которые можно сдать пользуясь этой структурой. Заранее благодарен !
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
14:13:47
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
14:13:47
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 30.11.2024 03:21:13 (k1).
Десктопная версия, переключиться на мобильную.
При поддержке
Я читал Википедию и код от Burunduk1. Splay-деревом решаётся как минимум всё то же самое, что и любым балансирующимся деревом поиска, потому что нет явных ограничений на дерево и splay-дерево, по сути, самое мощное из всех и умеет всё то, что умеют другие. Так что искать в сторону задач на, например, декартово дерево.
А нельзя ли сылочку на код ? Я видел в исходниках к VK Cup реализацию, на боюсь, там могут быть не все операции
Судя по плюсикам, не одному мне интересно . Дело в том, что сам уже написал примитивную реализацию, но наверное есть более "традиционный" код, который пишется быстрее, или, например, реализация более ефективная.
Учился по лекциям в параллели А+ ЛКШ.Зима. В английской википедии вполне прилично написано. Задачи — казалось бы, любая задача, где нужно двоичное дерево поиска? Я уже говорил, что можно считать себя умеющим писать любую деревянную структура данных если, например, сдал эту задачу с помощью неё.
Другой вопрос — зачем? Сплэй умеет не больше и не меньше, чем любое дерево поиска. Во всяком случае, всё, что он умеет, декартово дерево, наверное, тоже умеет.
UPD: а, блин... Правильно говорят, что я неправ. Мне спать пора.
Сплэй умеет строго больше, чем декартово. Хотя бы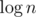
(жду коммент от Игоря =). А еще он не рандомизирован. Я верю, что можно придумать что-нибудь, что splay может, а декартово так же или проще — нет. Но это всё равно очень вряд ли пригодится на олимпиадах.
Dynamic Connectivitylinking-cutting trees заDynamic Connectivity? можно по подробнее здесь?
Черт, имелись в виду Linking-Cutting trees. Извиняюсь, в DC Splay вроде никак не помогает
Ок. теперь про Linking-Cutting trees можно подробнее? Из слов сказанных об этом на вики я не понял чем это отличаеся от декартового дерева, с его операциями Merge/Split. Можешь сформуливровать что это такое в паре предложений, суть только, а не то как оно делается.
Splay умеет такую штуку как make_root. Т.е. сделать вершинку корнем дерева. После запроса к какой-то вершине её делают корнем, и если обратиться к ней еще раз, то это произойдет быстрее. Утверждается, что если запросы происходят к K элементам, то среднее время запроса(по всем запросам) будет log K.
Splay — это самобалансирующееся дерево поиска без явных ограничений на структуру. Поэтому мы его можем менять как угодно, а потом вызвать expose() пару раз и всё станет хорошо. Но это лирика.
LCT, как известно, почему-то работают за
операций с деревом поиска. Если написать декартово, время работы будет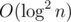 
. А вот если написать splay (который, вроде как, специально для этого и был придуман), то он очень хорошо самортизируется вместе с LCT и суммарное время работы получится 
, т.е. одна операция со splay будет работать в среднем за O(1) Вроде это получается рассуждениями в стиле "заметим, что если объединить корни splay'ев в большой лес по путям, то получается один большой splay", но я даже не знаю, как амортизировать обычный splay.
Спасибо за попытку, но должен сказать ты очень не ясно отвечаешь на вопросы, создавая еще больше вопросов. "LKT работают за ..." что есть LKT ? подразумевалось LCT? т.е. Linking-Cutting trees? Допустим ты опечатался и я угадал. тогда что означает "LCT работают за..."? имеется в виду серия запросов на разрезание/объединение? Извиняюсь если у меня одного существует такой пробел в знаниях, но я даже не понял что у декартового дерева работает за Log(n)^2
Самая главная операция в LCT – expose работает за log(n) splice'ов. Каждый splice работает за O(1) split и merge дерева. Поэтому если пути хранить в декартовом дереве один expose будет работать за log(n) ^ 2. Слейтор и Тарьян доказали, что если использовать Splay, то expose будет работать в среднем за log(n), то есть splice будет выполняться в среднем за O(1)
Поподробней про link-cut trees можно прочитать у их автора :
http://codeforces.me/blog/entry/2752#comment-63273