Построим любое остовное дерево минимального веса. Алгоритмом Крускала тем же. За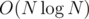

Допустим, мы умеем за 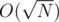отвечать на вопрос "Какой максимальный вес ребра от вершины A до какого-то её предка B".

Далее для каждого ребра, не входящего в это дерево: найдём наименьшего общего предка концов рёбер. Далее, найдём максимальный вес на этих двух путях — от каждого из концов до наименьшего предка. Очевидно, что он не может быть больше, чем вес рассматриваемого ребра — если он больше, то поменяв максимальное ребро на рассматриваемое, получили бы остовное дерево меньшего веса. Значит, если он меньше веса рассматриваемого ребра — рассматриваемое ребро "none". Если он равен весу рассматриваемого ребра — рассматриваемое ребро "at least one". "any", очевидно, оно быть не может, потому что изначальное дерево (одно из возможных) его не содержит. Если ребро "at least one", то также пометим на пути от концов к общему предку, что все рёбра данного веса надо пометить как "at least one" за .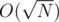

Когда все рёбра, не входящие в дерево, рассмотрены — для всех рёбер в дереве, помеченных "at least one" — ответ "at least one", для непомеченых — "any". "none", очевидно, не может быть, потому что изначальное дерево (одно из возможных) его содержит.

Детали реализации: Чтобы уметь находить максимальный вес и отмечать за 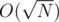, заметим следующее: Дерево фиксированно, и на любом пути дерева нас интересует только максимальный вес на этом пути.

Тогда будем хранить для каждой вершины её родителя, вес ребра до родителя, ближайшего предка с высотой кратной 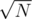, вес максимального ребра до этого предка. Тогда при ответе на вопрос "максимальное ребро в пути" идём с шагом 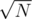, потом с шагом 1. Всего не больше 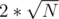шагов. Отмечаем так же — не каждую вершину, а отмечаем сначала с шагом 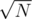— если вес максимального ребра совпадает с максимумом на пути, то "от этой вершини до родителя с номером, кратным 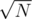все максимальные рёбра надо пометить "at least one". И потом для каждой вершины, где так записано, за те же 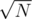проходим и по одному отмечаем рёбра.

Итоговая сложность решения .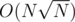

Вопрос: можно ли это в этом решении заменить корень на логарифм? (есть ли какое-то решение, идейно похожее на это, но за логарифм?)

Just in case: тут памяти линия. Понятно, что теоретически можно так же идти по длине по степеням двойки и для каждой вершины хранить логарифм предков и макс.весов — для каждой степени двойки. Но это вроде как-то не очень удобно и подобных реализаций я не встречал — таким методом за корень писать проще.