slycelote's blog

Codeforces Beta Round #14 tutorial
By slycelote, 14 years ago, In English

A. Letter

To find the smallest rectangle containing the picture, iterate through the pairs (i,j) such that the j-th symbol in i-th line is '*'; find the minimum and maximum values of i and j from these pairs. The rectangle to output is [imin, imax] × [jmin, jmax].

B. Young Photographer

First we find the intersection of all segments. To do this, denote by m the rightmost of left ends of the segments and denote by M the leftmost of right ends of the segments. The intersection of the segments is [m,M] (or empty set if m>M). Now determine the nearest point from this segment. If x0 < m, it's m, and the answer is m - x0. If x0 > M, it's M, and the answer is x0 - M. If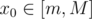 , it's x0, and the answer is 0. If m>M, then the answer is -1.

C. Four Segments

There must be many ways to solve this problem. The following one seems quite easy to code.
First count the number of distinct points among segments' ends. If it's not equal to 4, the segments can't form a rectangle and we output "NO". Then calculate the minimum and maximum coordinates of the 4 points: xmin, xmax, ymin, ymax. If xmin = xmax or ymin = ymax, then even if the segments form a rectangle, it has zero area, so we also output "NO" in this case.
Now if the segments indeed form a rectangle, we know the coordinates of its vertices — (xmin, ymin), (xmin, ymax), (xmax, ymin) and (xmax, ymax). We just check that every side of this rectangle appears in the input. If it is the case, we output "YES", otherwise we output "NO".

D. Two Paths

Take any pair of non-intersecting paths. Since Flatland is connected, there must be a third path, connecting these two. Remove a road from the third path. Then Flatland is divided into two components — one containing the first path, and the other containing the second path. This observation suggests us the algorithm: iterate over the roads; for each road remove it, find the longest path in both connected components and multiply the lengths of these paths. The longest path in a tree can be found by depth first search from each leaf.

E. Camels

Let us call an index j such that yj - 1  >  yj  <  yj + 1 a cavity. Also, we'll call humps and cavities by the common word break. Then there must be exactly T = 2t - 1 breaks, and the first one must be a hump.
Denote by fnth the number of ways in which a camel with t breaks, ending at the point (n,h), can be extended to the end (the vertical xN = N) so that the total number of breaks was equal to T. Note that:
1. fNTh = 1, if h=1,2,3,4. (We have already finished the camel and it has T breaks)
2. fNth = 0, if 0 ≤ t < T, h = 1, 2, 3, 4. (We have already finished the camel, but it has less than T breaks)
3. fn, T + 1, h = 0, if 1 ≤ n ≤ N, h = 1, 2, 3, 4. (The camel has already more than T breaks).
 
Now we find the recurrent formula for fnth. Suppose that t is even. Then the last break was a cavity, and we are moving up currently. We can continue moving up, then the number of breaks stays the same, and we move to one of the points (n + 1, h + 1), (n + 1, h + 2), ..., (n + 1, 4). Or we can move down, then the number of breaks increases by 1, and we move to one of the points (n + 1, h - 1), (n + 1, h - 2), ..., (n + 1, 1). This gives us the formula
.

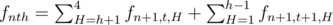If t is odd, then the last break was a hump, and similar reasoning leads to the formula
.

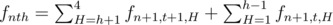We can calculate fnth by dynamic programming. Consider now the point (2, h) on a camel. There are h-1 ways to get to this point (starting from points (1, 1), ..., (1, h - 1)), and f2, 0, h ways to extend the camel to the end. So the answer to the problem is .
  • Vote: I like it
  • +19
  • Vote: I do not like it

Comments Comments (19)
| Write comment?
14 years ago, # |
  Vote: I like it 0 Vote: I do not like it
Great tutorial, thanks!
→ Reply
14 years ago, # |
  Vote: I like it 0 Vote: I do not like it
Thanks for the tutorial. But in problem C how do I determine 4 distinct points?
→ Reply
  • 14 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it
    For example, you can add all points to a set and then calculate its size.
    → Reply
    • 14 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it
      Can anyone help me make a complex set in C++?
      → Reply
      • 14 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it
        What do you mean? Have you tried std::set?
        → Reply
        • 14 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it
          Yes. Here's how:

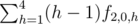          typedef complex<int> point;
          set<point> S;

          But it doesn't work. I can't insert any element using S.insert();
          → Reply
          • 14 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it
            "I can't do that" is a bad diagnostic. You should at least post error message. Also, it's useful to read the message yourself.

            Anyway. std::complex cannot be used with std::set, because it doesn't define operator<. Write your own struct or use std::pair.
            → Reply
            • 14 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it
              I'm done! Thank you honorable Captain adamax.
              → Reply
14 years ago, # |
  Vote: I like it 0 Vote: I do not like it
Nice tutorial. I like it so much. Thanks.
→ Reply
14 years ago, # |
  Vote: I like it 0 Vote: I do not like it

D. Two Paths

same question on spoj.pl but 2 ≤ N ≤ 100000 any idea how to solve.
→ Reply
  • 14 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it
    Could you post a link to the spoj problem?
    → Reply
  • 5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I believe my solution runs in $$$O(n\log{}n)$$$. There is a log factor because I am using sort(I believe I can get rid of it btw because I use it to pick the largest value and second-largest one in a vector). So in my solution, firstly I calculate the diameter of the tree using DP which means I obtain the answer for each node considering only nodes in its subtree in the tree rooted by an arbitrary node. Then, I use the rebooting technique of the tree following the order of the dfs. For each edge (u,v), I suppose it is cut and I calculate the diameter of the tree rooted by u but without the subtree rooted at v and since I have already calculated the diameter of the subtree rooted by v, I multiply these two values of diameters and keep the maximum result. Here is my code 74234280.

    → Reply
    • 4 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      If you keep the diameters of the subtrees and then you make an idea like rerooting: dp in-out, we can reduce it to $$$O(n)$$$ because in rerooting it would only change $$$O(deg (v))$$$ heights of nodes, right?

      We can solve this when we remove the information from the child to some root, at that moment it is as if the edge does not exist.

      → Reply
»
9 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

About the solution of problem E.

The first one must be a hump, also ** the last one must be a hump.**

So, fNth = 0, if0 ≤ t < T, h = 1, 2, 3.

BTW, when N + 2 < T, no camel with t humps exist, so the answer is 0.

→ Reply