Друзья, будьте бдительны!
Алгоритм Левита взятый с http://e-maxx.ru/algo/levit_algorithm работает в худшем случае за экспоненциальное время.
Для пояснения привожу код, который генерирует ацикличный граф без отрицательных ребер из 91 вершин и 121 ребра (а также перемешивает все ребра в случайном порядке), на котором код по ссылке выше делает более 1 000 000 добавлений в очередь.
const int M = 30;
const int W = (int)8e8;
void gen()
{
for (int i = 0; i < M; i++)
g[i].push_back(make_pair(i + 1, 0));
g[0].push_back(make_pair(M, W));
n = M;
for (int i = 0; i < M; i++)
{
g[n].push_back(make_pair(n + 2, W >> i));
g[n].push_back(make_pair(n + 1, 0));
g[n + 1].push_back(make_pair(n + 2, 0));
n += 2;
}
n++;
for (int i = 0; i < n; i++)
random_shuffle(g[i].begin(), g[i].end());
}
Какие выводы отсюда я хочу сделать? Не добавляйте в начало очереди, вся проблема в этом! Люди, добавляющие в начало очереди, рискуют однажды доиграться и попасться на хорошие тесты.
Если же вы хотите, чтобы ваш Форд-Беллман работал быстро — пишите обычного Форд-Беллмана с очередью, т.е. добавляйте вершины всегда в конец очереди и следите за тем, чтобы каждая вершина хранилась в очереди не более чем в одном экземпляре. Почитать можно здесь: http://wcipeg.com/wiki/Shortest_Path_Faster_Algorithm
P.S. В правильном "Левите" (см., например, книжку И.В.Романовского, Дискретный Анализ) использовалось 2 очереди. Описанный там алгоритм и правда работает за O(VE). Но от "Форд-Беллмана с очередью" не отличается (улучшение не более чем в 2 раза).
UPD:
Только что услышал такой способ искать кратчайший путь в графе с отрицательными ребрами:
Берем Дейкстру с кучей и запускаем на графе с отрицательными ребрами (при этом всегда, когда расстояние до вершины улучшается, кладем ее в кучу) :-) Казалось бы, этот алгоритм просто просмотрит каждую вершину несколько раз. На самом деле, он тоже работает за экспоненциальное время. Идея теста: давайте превратим ребра веса W в цепочки из двух ребер — веса 2k и (W — 2k). Далее строим такой же тест, как показан выше.











Сергей, если не секрет, что надоумило Вас анализировать этот алгоритм? Просто ради интереса, или кто-то напоролся на хороший тест?
Просто зашло обсуждение пока ехали в поезде, потому что об этой оптимизации было известно, что она хорошо улучшает в среднем, но непонятно почему работает вообще.
Паша правду говорит, в поезде СПБ-Петрозаводск оказалось, что я не умею доказывать оценку O(VE) для алгоритмов, добавляющих в начало. Оставлять это просто так было нельзя :-)
А что если не держать в очереди двух одинаковых вершин?
Если не класть в очередь вершину, которая уже в очереди, то эффект будет тот же.
Насколько реально построить двудольный граф в задаче о назначениях так, чтобы валился Левит (если мы решаем эту задачу через min-cost max-flow)?
Это очень просто. Возьмите таблицу умножения.
А как доказывается сложность левита при добавлении в конец?
Классический алгоритм Форд-Беллмана: будем V раз пытаться релаксировать все ребра.
Алгоритм Форд-Беллмана с очередью (также называемый "Левит с добавлением в конец"): будем на каждой из V итераций обрабатывать только ребра из тех вершин, расстояние которых улучшилось на предыдущей итерации (это как раз те вершины, что лежат в очереди).
Вроде бы очевидно, что второй алгоритм работает всегда не хуже, чем первый =)
Так было бы, если бы мы использовали две очереди (текущей итерации ФБ и новой), и добавляли с контролем дублирования во вторую. Здесь же мы в определенном случае релаксируем ребра "не вовремя", что может быть плохо (как в случае с добавлением в начало).
Ну у а как bfs работает Вы же понимаете? Там тоже в одной и той же очереди лежат вершины, до которых расстояние d, а потом вершины, до которых расстояние d+1.
Не-не, cooler содержательный вопрос задаёт. В отличие от bfs, в нашем случае вершина, расстояние до которой мы только что обновили, может оказаться далеко не в конце очереди (из-за того, что мы не кладём в очередь уже лежащую там вершину).
Ну...)))) Ну и что?) Если класть вершины всегда, памяти O(E), но зато работает так же, как и bfs. А теперь заметим, что если не класть, то хуже не станет. Кажется, все. Я не прав?
Ага, всё правильно :)
Ну всё равно этот ФБ быстро работает. Рассмотрим весь процесс и разобьём его на шаги: каждый шаг — это полный проход по очереди с предыдущего шага. Тогда утвержнение: на i-ом шагу для всех вершин, до которых есть кратчайший путь из ≤ i рёбер, расстояние найдено правильно. Доказательство несложное — база индукции очевидна, переход — если есть кратчайший путь из i рёбер вида ... - u - v, то на i - 1'ом шаге расстояние до u точно было правильным, а значит, до окончания i-ого шага u с правильным расстоянием хоть раз была извлечена из очереди (и из неё были проведены все возможные релаксации). А значит, расстояние до v посчитано правильно.
Подумал над этим внимательно, и понял весьма простое сведение одной очереди к двум независимым. Представим, что перед началом новой итерации мы релаксируем все вершины, которых нет в очереди этой итерации потому, что они в прошлой были последний раз обновлены до выхода. Будет, будто мы новую и старую итерации храним независимо. Но релаксация этих вершин ни к чему не приведет.
Вроде, разобрался, спасибо!
Пользуясь случаем, напишу про самый быстрый из известных мне вариантов Форда-Беллмана (насколько я помню, автор этого варианта — Tarjan).
Пусть мы хотим использовать алгоритм Форда-Беллмана не только для поиска кратчайших путей, но и для проверки того, есть ли в графе отрицательный цикл. Довольно естественная идея — искать циклы в метках from (которые обычно поддерживаются для восстановления кратчайших путей). В "нормальном" состоянии эти метки образуют лес, и если в этом лесе внезапно появился цикл — то это и будет отрицательный цикл в графе. Так что поддерживая лес меток from, можно быстро проверять, есть ли в графе отрицательные циклы.
Так вот, оказывается, если поддерживать этот лес в процессе алгоритма, можно его сильно ускорить следующим образом. Предположим, мы сделали релаксацию . У вершины v есть поддерево в нашем лесе, некоторые вершины {wi} которого могут лежать в очереди. Заметим, что поскольку мы только что прорелаксировали расстояние до v, все оценки расстояний до {wi} на данный момент неправильные, поэтому из них бесполезно делать релаксации, пока мы не обновим расстояния до них. Это наблюдение и даёт оптимизацию: после релаксации
. У вершины v есть поддерево в нашем лесе, некоторые вершины {wi} которого могут лежать в очереди. Заметим, что поскольку мы только что прорелаксировали расстояние до v, все оценки расстояний до {wi} на данный момент неправильные, поэтому из них бесполезно делать релаксации, пока мы не обновим расстояния до них. Это наблюдение и даёт оптимизацию: после релаксации  выкинем все вершины поддерева v из очереди и удалим из леса все рёбра поддерева.
выкинем все вершины поддерева v из очереди и удалим из леса все рёбра поддерева.
В итоге получается следующий рецепт: будем выполнять обычный алгоритм Форда-Беллмана с очередью, поддерживая лес меток from. При релаксации в какую-то вершину убиваем её поддерево в лесе, удаляя вершины этого поддерева из очереди.
Как ни странно, эта оптимизация в среднем даёт очень сильное ускорение — на больших графах "олимпиадного" размера (порядка 106 вершин) количество операций в десятки раз меньше по сравнению с версией без оптимизации.
Реализация алгоритма (автор — ilyaraz).
Класс! Я такого почему-то не знал =(
Илья, скажи, а тебе известны какие-нибудь оценки снизу на асимптотику алгоритма, который ищет кратчайшие пути в графе с отрицательными ребрами?
Не, никаких нижних оценок не знаю. Из верхних — есть потокообразный адъ за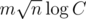 (C — ограничение на вес, веса целые), но этот алгоритм сложно закодить и он проигрывает ФБ с эвристикой Tarjan'а.
(C — ограничение на вес, веса целые), но этот алгоритм сложно закодить и он проигрывает ФБ с эвристикой Tarjan'а.
Удачных челленджей и взломов =)
Надо признать, что мне писали об этом на почту, но я всё не находил времени сесть разобраться... Да и во всяких научных статьях конкретно того "Левита", что у меня, я не находил, поэтому оставалась надежда, что он всё же полиномиальный.
Эх, жалко, такой ведь забавный алгоритм был :)
P.S. Да и всё равно не отнять у него скорости работы на случайных тестах или некоторых графах особого вида (например, граф переходов по клеткам клетчатого поля) — обычное дело, когда на тестах жюри он отрабатывает быстрее Дейкстры :)
Вот :) Меня поймать, слава Богу, никто не успел
Видимо следует "быть бдительным" и по отношению к статье "Поток минимальной стоимости" (http://e-maxx.ru/algo/min_cost_flow) так как "приведена реализация алгоритма min-cost-flow, базирующаяся на алгоритме Левита.".
Хотя, если честно, последние год — полтора во всех задачах, где нужен был min-cost-max-flow, я писал этот алгоритм и он прекрасно работал и получас АС.
дейкстру ещё надо уметь написать так чтобы он работал с отрицательными весами рёбер.
Да, потенциалы нужны
а есть где-нибудь где об этом почитать можно?
Здесь (вторая ссылка).
ваша ссылка не работает
Работает
Могу ошибаться, но вот тут написано, что этот алгоритм в худшем случае и работает за экспоненту.
Еще на тему.