KADR's blog

Codeforces Beta Round #13 editorial
By KADR, 15 years ago, translation, In English

Let me introduce an editorial to Codeforces Beta Round #13. If you have any questions or propositions - feel free to post them in the comments.


Problem A.
It is sufficient to iterate over all bases from 2 to A-2 and find the sum of digits in them. Then one should find the greatest common divisor of found sum and A-2 (which is equal to number of bases in which we found the sums). The numerator of the answer is equal to founded sum divided by this GCD and the denominator is equal to A-2 divided by this GCD.

The complexity is O(A).

Problem B.
This problem appeared to be quite unpleasant to code, but all what one need to do is to check whether all three statements are true. It is recommended to perform all computations using integer arithmetics and to use scalar and vector product instead of computing cosines of angles or angles itself.

Problem C.
Note, that there exists a non-decreasing sequence, which can be obtained from the given sequence using minimal number of moves and in which all elements are equal to some element from the initial sequence (i.e. which consists only from the numbers from the initial sequence).

Suppose {ai} is the initial sequence, {bi} is the same sequence, but in which all elements are distinct and they are sorted from smallest to greatest. Let f(i,j) be the minimal number of moves required to obtain the sequence in which the first i elements are non-decreasing and i-th element is at most bj. In that case the answer to the problem will be equals to f(n,k), where n is the length of {ai} and k is the length of {bi}. We will compute f(i,j) using the following recurrences:

f(1,1)=|a1-b1|
f(1,j)=min{|a1-bj|,f(1,j-1)},  j>1
f(i,1)=|ai-b1|+f(i-1,1),  i>1
f(i,j)=min{f(i,j-1),f(i-1,j)+|ai-bj|},  i>1, j>1

The complexity is O(N2). To avoid memory limit one should note that to compute f(i,*) you only need to know f(i-1,*) and the part of i-th row which is already computed. 

Problem D.

We will solve the problem using the following algorithm:
  1. Fix some red point.
  2. Find the number of triangles with vertices in the red points which don't contain any blue points inside and which have the fixed red point as one of the vertices.
  3. Remove the fixed red point and go back to statement 1, if there remain any red point.
The first and third statements are obvious, so the main part of the solution is statement 2.

Suppose the red point A is fixed (in the first statement). Also suppose we have all other points which are still not removed (blue and red together) sorted by angle around the point A. We will iterate over all red points B, which will be the second vertice of triangle. Now, we need to find the number of triangles with vertices in red points which have points A and B as two vertices and which don't contain any blue point inside.

To solve this problem we will iterate over all unremoved points C in the increasing order of angle ABC starting from the point after the point B (in the same order). To avoid double counting we will stop when the angle between vectors AB and AC become greater than 180 degrees or when we reach the point which was already considered. Then we will perform such actions:
  • If C is red then we will check whether there are blue points inside triangle ABC and if not - we will increase the answer by 1. Note, that to perform this check we don't need to iterate over all blue points. It is sufficient to maintain such point D from the ones which we have already seen for which the angle ABD is the smallest possible. If D doesn't lies inside the triangle ABC, then there is no blue point which lies inside it.
  • If C is blue, then we will compare the angle ABC with ABD and if ABC is smaller, we will replace old D with C.
Note, that after choosing new B we consider that there is no point D and there will be no blue points inside triangles ABC until we reach the first blue point.

The complexity is O(N2(N+M)). 

Problem E.

Let's divide all row into blocks of length K=sqrt(N) of consecutive holes. If N is not a complete square, then we will take K=sqrt(N) rounded down. For each hole we will maintain not only it's power (let's call it power[i]), but also the number of the first hole which belongs to other block and which can be reached from the current one with sequence of jumps (let's call it next[i]). Also, for each hole we will maintain the number of jumps required to reach the hole next[i] from the current one (let's call it count[i]). We will consider that there is a fictious hole, which lies after the hole N and it belongs to it's own block.

To answer the query of the first type (when the ball is thrown) we will jump from the hole i to hole next[i] and so on, until we reach the fictious hole. Each time we will add count[i] to the answer. We will jump not more than N/K times.
To maintain the query of the seqond type (when the power of hole i is changed) we will change power[i], next[i] and count[i]. Then for each hole which belongs to the same block as i and has smaller number than i we will update next[i] and power[i] in decreasing order of number of the hole. We will perform not more than K updates.

The complexity is O(Nsqrt(N)).
  • Vote: I like it
  • +27
  • Vote: I do not like it

Comments Comments (21)
| Write comment?
15 years ago, # |
  Vote: I like it 0 Vote: I do not like it
There are some good solutions about the problem C,whose run time is 30 ms. I think these solutions' complexity is less than O(N^2). But I can't understand these solutions' main idea. Do you understand those solutions?

Thanks,
Jianfei
→ Reply
15 years ago, # |
  Vote: I like it +3 Vote: I do not like it
Thanks for the editorial.

There is another way to solve problem D. You can count the amount of points (x, y) below each segment (ax, ay) - (bx, by) with ax ≤ bx such that ax < x ≤ bx in O(N2M) and store these values in a table. Then you can compute the result by iterating over all triangles and counting the points inside the triangle in O(1) using the values stored in this table.
→ Reply
15 years ago, # |
  Vote: I like it 0 Vote: I do not like it
Can you explain the following statement? Thanks
About Problem C.
Note, that there exists a non-decreasing sequence, which can be obtained from the given sequence using minimal number of moves and in which all elements are equal to some element from the initial sequence (i.e. which consists only from the numbers from the initial sequence).
→ Reply
  • 15 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it
    Suppose there is no optimal sequence where each element is equal to some element from the initial sequence. Then there is an element i which is not equal to any of the elements of {ai}. If the elements with numbers i-1 and i+1 are not equal to element i, then we can move it closer to ai and the answer will decrease. So there is a block of equal elements and all of them are not equal to any of the elements of the initial sequence. Note, that we can increase all block by 1 or decrease it by 1 and one of this actions will not increase the answer, so we can move this block up or down until all its elements will be equal to some element from the initial sequence.
    → Reply
13 years ago, # |
  Vote: I like it 0 Vote: I do not like it
Nice solution for problem C.
But i think following statement is not true.Do you agree with me?
Let f(i,j) be the minimal number of moves required to obtain the sequence in which the first i elements are non-decreasing and i-th element is equal to bj
I think it must be like that:f(i,j) is the minimal number of moves required to obtain the sequence in which the first i elements are non-decreasing and i-th element is at most bj.(can be equal to any of bk, while k=1,2,...,j-1,j)
Note that:
f(i,j)=min{f(i,j-1),f(i-1,j)+|ai-bj|},  i>1, j>1.
→ Reply
  • 13 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it
    Thank you. I've fixed this in the post, though for some reason it was correct in the Russian version.
    → Reply
»
12 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In Problem E: lets save for each hole the answer , number of jumps after ball leaves this hole and the last hole for it. Then for each query we have answer in o(1) and for each update of strength we can look the hole which will be after this hole . ((new strength)+i) and rewrite its answer to this hole and increase the first answer (number of jumps ) by 1 and second answer (last hole) will be same. This is o(M) solution . Any mistake ?

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Do you really think that problem E can be that easy? After updating the strength of the hole number X the answer will change not only for the hole X, but also for all holes Yi from which X is reachable by 1 or more jumps. The number of such holes Yi is O(N).

    → Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem C :in which all elements are equal to some element from the initial sequence

Why? to get the min step , the final sequence 's every number is same to the initial sequence?? why is this optimal? Thanks.

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    Well, to be more precise, we can say that there IS an optimal final sequence whose numbers are all from the original sequence, which can be proved by contradiction. Take the original sequence "3 1" for example. Although "2 2" is an optimal one whose numbers are not from the original sequence, "1 1" or "3 3" is optimal and their numbers are from the original one.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

kadar not able to visualize the solution can you please help me do that ?

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can someone please give me a good link for square root decomposition.

i found various links on google but don't know which one is good and contains all details on sqrt decomposition.

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem E can also be solved using the Link-cut tree in .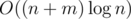

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Anyone noticed that Problem E also required the number of the last hole the ball visited?

So we'll have to jump to the block before we jump to the fictious hole and jump to the last hole before we jump to the fictious hole. So I had to add another while loop.

But it seems that the complexity is the same? Well, I'm just here to say that the type 1 query is not that easy(probably still easy for great coder,but not for this noob)

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    And I've got a TLE on test 13.Anyone help me?

    /*
ID: jerrywcy
LINK: http://codeforces.me/contest/13/problem/E
LANG: C++
STATUS:
*/
#include <bits/stdc++.h>

#define init(array,x) memset(array,x,sizeof(array))

using namespace std;

const int inf=0x3f3f3f3f;
const int maxn=100010;

int n,q;
int a[maxn];
int m,len;
int l[1010],r[1010];
int pos[maxn],nxt[maxn],step[maxn];

void build(){
	m=len=sqrt(n);
	for (int cur=1;cur<=m;cur++){
		l[cur]=len*(cur-1)+1;
		r[cur]=len*cur;
		for (int i=l[cur];i<=r[cur];i++){
			pos[i]=cur;
			int j=i;
			while (j<=r[cur] && j<=n){
				j=min(j+a[j],n+1);
				step[i]++;
			}
			nxt[i]=j;
		}
	}
	if (r[m]!=n){
		m++;
		l[m]=r[m-1]+1;
		r[m]=n;
		for (int i=l[m];i<=r[m];i++){
			pos[i]=m;
			int j=i;
			while (j<=r[m] && j<=n){
				j=min(j+a[j],n+1);
				step[i]++;
			}
			nxt[i]=j;
		}
	}
	return ;
}

void add(int x,int y){
	int bl=pos[x];
	a[x]=y;
	for (int i=x;i>=l[bl];i--){
		nxt[i]=max(nxt[i+a[i]],n+1),step[i]=step[i+a[i]]+1;
	}
	return ;
}

void query(int x){
	int cnt=0;
	while (nxt[x]<=n){
		cnt+=step[x];
		x=nxt[x];
	}
	while (x+a[x]<=n)x+=a[x],cnt++;
	printf("%d %d\n",x,cnt+1);
	return ;
}

void solve(){
	int opt;
	scanf("%d",&opt);
	if (!opt){
		int x,y;
		scanf("%d %d",&x,&y);
		add(x,y);
	}
	else{
		int x;
		scanf("%d",&x);
		query(x);
	}
}

int main()
{
	scanf("%d %d",&n,&q);
	for (int i=1;i<=n;i++)scanf("%d",&a[i]);
	build();
	while (q--)solve();

	return 0;
}
    → Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

solve C

$$$O(n \log n)$$$
→ Reply
»
7 weeks ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem E, but also the number of the first hole which belongs to other, do the number here refer to the smallest index of hole in which are residing in different segment and also could be hopped on through a series of jump ?

→ Reply
»
4 weeks ago, # |
  Vote: I like it 0 Vote: I do not like it

I did E using square root decomposition (Divided the array into blocks of size sqrt(n), then for each element stored only the last index within its block after which it jumps to an element in another block or out of the array).

My O(n * sqrt(n)) solution is getting TLE on testcase 16. Can anyone help? 285297411

→ Reply
»
4 weeks ago, # |
← Rev. 9   Vote: I like it 0 Vote: I do not like it

I'm getting a Wrong Answer (WA) on test case 3 while using Square Root Decomposition. Can anyone help me figure out why? For the problem E **** //

include<bits/stdc++.h>

define ll long long

define endl "\n"

using namespace std;

vector<map<ll, pair<ll, ll>>> mp; ll flg[100005]; ll arr[100005]; ll n, k; vector<pair<ll,ll>>combi;

void findd() { ll l; cin >> l; ll val = 0; while (1) { ll com = flg[l]; val += mp[com][l].second; if (mp[com][l].first == l || com == 0) { cout << mp[com][l].first << " " << val << endl; break; } else l = mp[com][l].first; } }

void update(ll i) { ll e = combi[i].first; ll s = combi[i].second; map<ll, pair<ll, ll>> mm; for (ll j = e; j >= s; j--) { ll p = arr[j] + j; if (p > n) p = j; mm[j] = {p, 0}; if (flg[j] == flg[p]) { mm[j].second = mm[p].second + 1; mm[j].first = mm[p].first; } else mm[j].second = 1; } mp[i] = mm; }

void out() { ll i=0; for (auto v : mp) { cout<<"block "<<i<<endl;i++; for (auto p : v) { cout << p.first << " = " << p.second.first << " " << p.second.second << endl; } cout << endl; } }

int main () { ios_base::sync_with_stdio(0); cin.tie(0); cin >> n >> k; for (ll i = 1; i <= n; i++) cin >> arr[i]; ll x = sqrt(n); mp.resize(x+2); ll cnt = 0; ll s = 0; pair<ll,ll>pp; for (ll i = n; i > 0; i--) { if(cnt==0)pp.first=i; cnt++; flg[i] = s; if (cnt == x || i==1) {pp.second=i;combi.push_back(pp); cnt = 0; s++; } }

// update all from end;
for(ll i=0;i<combi.size();i++)
update(i);


for (ll i = 0; i < k; i++) {
    ll t; cin >> t;
    if (t == 1) findd();
    else if (t == 0) {
        ll i; cin >> i >> arr[i];
        update(flg[i]);
        //out(); 
    }
}

} // ****

→ Reply