sin 1 + sin 3 + sin 5 + sin 7 + sin 9 + ...
Any ideas? PD: The angle is in radians.
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3857 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 165 |
| 2 | -is-this-fft- | 161 |
| 3 | Qingyu | 160 |
| 4 | Dominater069 | 158 |
| 5 | atcoder_official | 157 |
| 6 | adamant | 155 |
| 7 | Um_nik | 151 |
| 8 | djm03178 | 150 |
| 8 | luogu_official | 150 |
| 10 | awoo | 148 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Mar/04/2025 14:11:08 (k1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











If you have no clue about a summation, Wolfram Alpha will save your butt. Link
Apperently a closed formular for the first
n + 1elements is:sin(n+1)^2/sin(1). I guess you can prove this formular using induction and a few trigonometrical identities.sin α = Re(eiα)
Lol, I have written my previous post 4 days ago, got 22 upvotes and nobody pointed out, that there should be Im instead of Re :P. Btw even given that equality, I still don't know how to compute that sum : D.
You have a sum of geometric progression inside Im, you may calculate its sum in O(1) as some fraction and explicitly express its imaginary part by carefully dividing numerator by the denominator.
OK, that geometric progression is what I had in my mind when I was writing first post, but somehow I got stuck when computing imaginary part of [tex_crapped_on_cf]\frac{e^{(2n+1)i} — e^i}{e^{2i} — 1}[\tex_crapped_on_cf], but of course it can be done.
It is good idea to multiply this by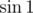 or
or 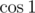 (because, for example,
(because, for example, 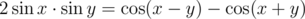 and there will be a lot of summands that "kill" each other, it is general way to simplify such sums) to get telescopic series, let's multiply (for example,
and there will be a lot of summands that "kill" each other, it is general way to simplify such sums) to get telescopic series, let's multiply (for example, 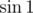 , it works better in this case):
, it works better in this case):
So,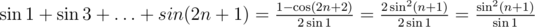 .
.