How to solve the problem from latest Codechef Long Contest :
Скоро Codeforces Round 1133 (Div. 1, Div. 2)! Регистрация здесь.
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | Benq | 3676 |
| 2 | Kevin114514 | 3659 |
| 3 | jiangly | 3640 |
| 4 | turmax | 3450 |
| 5 | tourist | 3382 |
| 6 | strapple | 3360 |
| 7 | Um_nik | 3354 |
| 8 | squareOf105 | 3348 |
| 9 | maroonrk | 3312 |
| 10 | idontwannadothis…e | 3191 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | Qingyu | 155 |
| 2 | nik_exists | 151 |
| 3 | maspy | 149 |
| 4 | AmShZ | 145 |
| 5 | Um_nik | 143 |
| 6 | Errichto | 139 |
| 7 | BledDest | 136 |
| 8 | adamant | 134 |
| 9 | maroonrk | 132 |
| 10 | cry | 130 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2026 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 06.11.2026 23:02:10 (g2).
Десктопная версия, переключиться на мобильную.
При поддержке
Let's think of a way construct a permutation: Initially, it's empty. One by one, we add an element. Assume, after that we have permutation p1, p2, ..., pk and pi is recent element. So, we must have: p[i-1] + d > p[i], p[i] + d> p[i+1]. If the sequence we add is non-decreasing, then we just care about the condition p[i-1] + d > p[i]. Clearly, the way we add pi equals to the number of element before pi (in sorted non-decreasing sequence) that greater than p[i]-d and plus one for adding at first position. (*) Therefore, we have a solution in O(m * n * log(n)). In order to improve that complexity, in each query, we maintain the number (*) for each element. And in each query, there are O(D) element is affected. Complexity reduce to O((n + m) * d).
But how are we counting the number of valid permutations using the above logic, Could you please elaborate your solution ??
It's the product of them. Example, we have sequence: 1, 3, 4, 7, 9 and d = 3. There is no number less than 1 and greater than 1 — 3. There is one number less than 3 and greater than 3 — 3. There is one number less than 4 and greater than 4 — 3. There is no number less than 7 and greater than 7 — 3. There is one number less than 9 and greater than 9 — 3. So the answer in this case is: (0 + 1) * (1 + 1) * (1 + 1) * (0 + 1) * (1 + 1).
I got the approach, But what is the intuition behind this counting approach ??
Thanx got it :)
My solution is complicated. Let's maintain cnt[i] count the number of sequence equals to i in each query. Because, each element can be large as 10^9, so we must decompress them. After having cnt[i] for each i, we will be able to count the number of way add cnt[i] numbers value 'i' in the above way.
How to solve WRDSUM?
Use inclusive-exclusive principle: Almost always F(n) = n. So we start with 2 + ... + n. Let's look how to fix our sum
we have to subtract
and put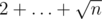 
instead.
we have to subtract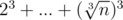
and put 
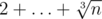instead.
we have to subtract
and 
and put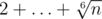
, and 
instead.
And so on. If you calculate this properly you will get sth like this
The formula 2d + ... + xd is a polynomial of degree d + 1 so we can use Lagrange interpolation to get coefficients, or precompute Bernoulli numbers and use Faulhaber's formula. Notice that max D is around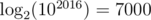
.
Depending on implementation we should get sth like O(D2) or even faster solution. Use python or java to avoid bignum implementation.