Hi,
Can anyone help me with this problem?
You are given an array with n integers a1, a2, ..., an , a integer K and m queries.
There are two types of query:
give you two integers l and r and ask you to print how many number of integers al, al + 1, ..., ar which equal to K.
give you three integers l, r and v and ask you to add the value of al, al + 1, ..., ar by v.
You should print the answer of the first queries.
Thanks, Sorry for my bad English!











Do you know how to solve the second type of queries ?
It can be done with segment trees (Lazy propagation). but I don't have a good idea to solve both types of queries.
I've proposed such a problem for a contest several years ago. After a long discussing with IGMs I strongly believe (but still have no proof) that this problem can be solved only be SQRT-decomposition in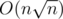 .
.
Basic idea: split an array into several chunks of size , for each chunk store a multiset of numbers in it and a (lazy-propagated) value which should be added to each of them.
, for each chunk store a multiset of numbers in it and a (lazy-propagated) value which should be added to each of them.
Why no proof? What's wrong with this solution?
I think we can do it using segment tree. Store at each Node Merge Sorted array of its children with two extra variables one for lazy and let the other be named to_subtract.
Use Lazy propagation!
At each query instead of finding K you have to find the frequency of number = K-to_subtract . This can be done in O(LOG N ) using upper bound and lower bound on the saved array as it was sorted once!
Note : during the process we never change the array! So the complexity will be O(Log N ^ 2)
Your code fails on this case: N = 4, and array is {1, 1, 1, 1}.
First query is +1 in [1, 2].
Second is number of 1s in [1, 4].
Your idea will print 4 instead of 2.
Yeah you are right! I was thinking of same query as the update operation!
We will have to update the array ! So the approach is totally useless !
As far as I know it is impossible to solve general problem in O(n * log(n)).(I remember that Haghani said that is impossible, but not I'm not sure).
But it can solved in O(n * sqrt(n)) easily.also if you have an array of K's you can done it in O(n * sqrt(n) * k).
But there is one case of problem that can be solved in O(n * log(n)) if we know that K is always smaller(or greater) than all of ai s. keep in segment node a pair: {frequency_of_minimum,minimum}.