C137's blog

Geometry problem
By C137, history, 9 years ago, In English

Hello everyone

I am facing the following geometry problem, and since am not so good at it, i would ask your help:

We have a straight line that goes throw 3 points, A(X1,Y1) B(X2,Y2) and M(X0,Y0).

We know X1,Y1,X2,Y2 and we know d, the distance between A and M, and we have to define the two possible positions of the pair X0,Y0...

Any Help would be highly appreciated, and thanks in advance...

  • Vote: I like it
  • -6
  • Vote: I do not like it

»
9 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Here is O(1) solution with some inaccuracy permitted:

You know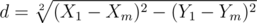

You also know slope of line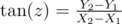

So, the two possible values of Xm are X1 ± d * cos(z)

Similarly, Ym = Y1 ± d * sin(z)

→ Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You can explain little more pls.....

    → Reply
    • »
      »
      »
      9 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      from the image you can say that sin(z)= (y0-y1) / d from this equation you can say that sin(z)*d = y0-y1 so: y0 = y1 + d*sin(z) but y0 may also be in the other direction so y0=y1(+or-)d*sin(z) also you can notice that cos(z)=(x0-x1)/d from this you can say that x0=x1(+or-)d*cos(z) and you can calculate z since that tan(z)=slope which equals to (y2-y1) / (x2-x1) you can make tan inverse to get z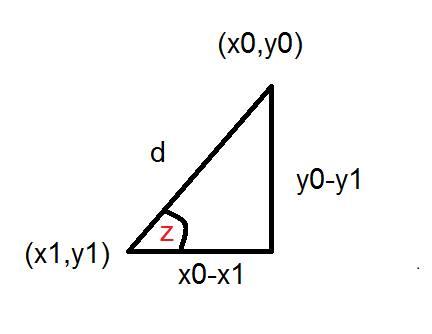

      → Reply
  • »
    »
    9 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    thanks

    → Reply
»
8 years ago, # |
  Vote: I like it -15 Vote: I do not like it

.

→ Reply