Задачи учебные — постараемся сделать разбор подробным.

598A - Tricky Sum

Если бы в этой задаче не было бы "хитрости" и надо бы было просто найти сумму 1 + 2 + ... + n, то, воспользовавшись формулами суммирования арифметической прогрессии, можно было прийти к результату s = n·(n + 1) / 2 (числа такого вида называются треугольными).

Однако каждое число, которое является степенью двойки, должно быть просуммировано не со знаком "плюс", а со знаком "минус". Давайте вычтем по два раза (так как первое вычитание просто изымет число из суммы, а второе — вычтет) каждую из степеней двойки, которые не превосходят n. Проще всего это сделать с помощью цикла вроде этого:

long long pow2 = 1;
while (pow2 <= n)
    s -= pow2 * 2, pow2 *= 2;

Значение s после такого цикла и будет ответом. Количество итераций этого цикла не превосходит двоичного логарифма числа n (точнее — еще плюс единица), что является числом около 30 для максимального возможного теста.

Асимптотика: (на один тест в наборе).

598B - Queries on a String

Так как значения k_i довольно велики (до миллиарда), то попробуем найти решение, которое не моделирует все k_i вращений. Очевидно, что если рассматривать k-й циклический сдвиг строки длины t, то все сдвиги, кратные t, не меняют строку. Более того, k-й циклический сдвиг строки длины t неотличим от сдвига на величину k mod t (остаток от деления k на длину t).

Таким образом, сразу после чтения очередного запроса можно заменить k_i на k_i mod (r_i - l_i + 1). Далее определим результат после запроса i. Части строки до l_i и после r_i останутся без изменения. А вот подотрезок l_i... r_i провернётся на k_i. Это значит, что вперед встанут заключительные k_i символов этой подстроки, а потом — часть подстроки без заключительных k_i. В итоге обработанный подотрезок будет записан так: s.substr(r - k + 1, k) + s.substr(l, r - l + 1 - k) (участок длины k от позиции на k - 1 левее r + участок длины "длина подотрезка минус k" от позиции l). Следовательно, весь запрос обрабатывается фрагментом кода:

s = s.substr(0, l)
    + s.substr(r - k + 1, k) + s.substr(l, r - l + 1 - k)
    + s.substr(r + 1);

Конечно, в данной задаче удобнее было бы воспользоваться функцией std::rotate, от этого код стал бы только короче. Однако такой подход более С++-специфичный. Эквивалентная строка с использованием std::rotate выглядит так: rotate(s+l,s+r+1-k,s+r+1);.

Асимптотика: O(|s|·m).

598C - Nearest vectors

На этой задаче споткнулись очень многие участники. Некоторые даже очень опытные участники соревнований допустили ошибки. Видимо, эта задача проходит с использованием atan2 в long double на g++ (но не на Visual Studio, так как в ней long double имеет такой же размер как и double — 8 байт).

Я опишу здесь решение в целых числах, которое, безусловно, неплохо понимать и знать.

В своих решениях с несложной геометрией я люблю использовать typedef pair<T,T> pt (где T — основной тип данных для точки/вектора), одновременно с дефайнами X на first и Y на second.

Грубо говоря, план решения такой: отсортируем все вектора по полярному углу, затем переберем все пары соседних векторов и выберем такую, угол между векторами в которой минимален.

Для того, чтобы отсортировать что-либо, надо определить функцию порядка "меньше" (возвращает true тогда и только тогда, когда первый аргумент строго меньше второго).

Ниже будем использовать псевдоскалярное произведение векторов (cross(a, b) = a.X * b.Y - a.Y * b.X), которое для простоты будем называть просто векторным. Напомним, что оно равно |a|·|b|·sin(a, b), где sin(a, b) — синус ориентированного угла от первого вектора ко второму. Поэтому знак векторного произведения указывает "верно ли, что угол от первого до второго вектора меньше 180 градусов?" или (что тоже самое) "верно ли, что кратчайший способ совместить (сонаправить) первый вектор со вторым будет двигать первый вектор против часовой стрелки?". Когда величина равна 0 — это значит, что всё равно, как: то есть вектора либо сонаправлены, либо противонаправлены.

Поэтому, чтобы понять, верно ли, что при сортировке первый вектор должен предшествовать второму, почти всегда достаточно посмотреть на знак векторного произведения (больше нуля — значит, "да"). Однако это не будет работать на стыке при переходе через цикл (например, вектор (1, -1) будет определен как стоящий до вектора (1, 1)). Для этого сначала сравним полуплоскости, в которых они расположены (при Y = 0 в верхнюю полуплоскость отдадим положительное направление луча Ox). Функция top определяет "верно ли, что p лежит в верхней полуплоскости?".

bool top(pt p) {
    return p.Y < 0 || p.Y == 0 && p.X < 0;
}

Следовательно, полностью функция "меньше" для сортировки векторов по полярному углу в целых числах выглядит так:

bool polarLess(const pt& a, const pt& b) {
    bool ta = top(a);
    bool tb = top(b);
    if (ta != tb)
        return ta;
    return cross(a, b) > 0;
}

Теперь решим вторую подзадачу — для четырех векторов a₁, b₁, a₂ и b₂ проверить, верно ли, что угол между a₁ и b₁ строго меньше угла между a₂ и b₂.

Напомним, что неориентированный угол между векторами a и b можно получить так: представим, что мы расположили оба вектора так, что вектор a встал по направлению Ox (т.е. просто вправо). Тогда будет достаточно найти полярный угол для b (координату b.Y надо взять по модулю, так как угол неориентированный). Но вектор a не направлен вдоль Ox. Давайте найдем длину проекции b на a (это на самом деле x в системе координат, что направлена так, как нам хочется) и длину проекции b на вектор, повернутый от a на 90 градусов (перпендикулярный) влево. Длину первой проекции найти легко — это |b|·cos(a, b), а длина второй проекции — это |b|·sin(a, b). Однако, если мы возьмем просто скалярное произведение, то получим |a|·|b|·cos(a, b), а векторное — |a|·|b|·sin(a, b).

То есть вектор p = (dot(a, b), cross(a, b)) (где dot(a, b) — скалярное произведение) — это вектор, сонаправленный вектору b' (где b' — результат поворота вектора b, если одновременно вращать и b и a так, что a совпадет с Ox). Здесь хорошо бы сделать рисунок, но уже не до этого.

Таким образом, например, чтобы найти ориентированный угол между векторами (от  - π до π), достаточно взять направление вектора p; иными словами, atan2(cross(a, b), dot(a, b)). Если нужен угол неориентированный, то от векторного произведения (а это фактически координата y у вектора p) надо взять модуль.

Теперь найдем пару векторов p₁ и p₂, как описано выше, затем посмотрим, кто из них образует меньший полярный угол. Это можно сделать с помощью уже знакомого свойства векторного произведения.

Таким образом, полный код функции "меньше" для величины угла между векторами a₁ и b₁ против величины угла между векторами a₂ и b₂ выглядит так:

bool angleLess(const pt& a1, const pt& b1, const pt& a2, const pt& b2) {
    pt p1(dot(a1, b1), abs(cross(a1, b1)));
    pt p2(dot(a2, b2), abs(cross(a2, b2)));
    return cross(p1, p2) > 0;
}

Асимптотика: 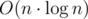(на сортировку).

598D - Igor In the Museum

Здесь надо подробнее описать, что нужно обходить поиском в глубину компоненту связности лабиринта, причем каждую не более одного раза. Во время обхода подсчитывать количество картин и хранить это прямо по индексу компоненты. Если запрос пришел про клетку, для которой уже обработали ее компоненту, то забираем ответ по номеру компоненты. Вот пример простого короткого решения 14257172.

Асимптотика: O(n·m + k) (каждая клетка обходится не более одного раза).

598E - Chocolate Bar

Здесь надо подробнее описать динамическое программирование, которое используется в решении. В решении ниже dp[a][b][k] — ответ на задачу, если есть плитка размера a × b и надо наотламывать k долек из нее. В приведенном решении используется ленивое программирование (каждое состояние анализируется фактически не более раза с помощью поиска в глубину по состояниям) для подсчета таких значений: 14258732.

Асимптотика: 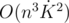(K — оценка на k, то есть 50).

598F - Cut Length

Эту задачу я когда-то давно подготовил на тренировку СГУ. Ее сдали несколько наших сильных участников (возможно, в дорешку): Nerevar, e-maxx, RAD, stan, NALP. По результатам взломов — все их решения оказались неверными! Участники Educational Codeforces Round 1 добавили отличные тесты!

Вот короткое решение одного из участников раунда (и эффективного взломщика): 14258627.

Асимптотика: 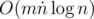(для обработки одной прямой нужна сортировка всех точек пересечения её и многоугольника).

Заключение

Я буду рад дать права на пост тому, кто поможет перевести разборы или улучшит наброски разборов по задачам D-F. Спасибо!