I mean proven things like comparison sort can't have an asymptotic better than N * log(N). I haven't ever heard about other similar cases. Is there anyone who knows?
UPD: probably I did not describe the question properly enough, although zxqfl gave an answer I expected to get. I have meant that we have some sort of problem with strict restrictions, for example finding a minimal path from S to T in a graph with 1 ≤ w(e) ≤ 109 integer length of all edges and this is proven that this task can not be solved faster than in O(M * logN) or something like that. (Not exactly saying I know how to prove this, just giving an example)
well it's an easy fact that if your algorithm is O(f(n)) and input is also O(f(n)) then ur algorithm is the best :) coz u need O(f(n)) things to read . so all DFS , BFS , KMP , ... are the best algorithms :)
Given a weighted connected graph (V, E, w) such that for all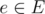
we have w(e) = 1, how much time do you need to determine the weight of the minimum spanning tree? How much time do you need to read the input?
QFT works in polynomial time of log(n) for array of size n. This one is more crazy.
Actually, in computer science, n is always the size of input. So what you are saying is nonsense. DFS, BFS and KMP are not O(n) necessarily (for example, I give you a special graph like Kk, so
, and when you run DFS on it, it's O(k2) which is O(22n) which is exponential time).
That's why the algorithm that checks if a number m is prime or not in
is not polynomial (because 
and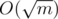 
= O(2n / 2) which is not a polynomial of n).
Lol, it was clearly meant to be on graphs with all its edges given on input. If you really want to, for any problem I can create a sequence of inputs I1, ..., such that size of In is nnnnnnnn and give you n as new input and expect solving original problem on instance In, but that doesn't make any sense and your DFS example is more or less the same thing.
Given that P ≠ NP, edit distance can't be solved in O(n2 - δ) for δ > 0.
http://arxiv.org/abs/1412.0348
(Technically the result they used isn't exactly P ≠ NP but it's very similar)
Due to Mihai Patrascu, dynamic partial sums (with point updates) require
memory probes, thus making balanced trees an optimal solution. Take a look at his thesis for more lower bounds.
That is a really very interesting question, I also asked it myself few times. Proving nonlinear polynomial lower bounds on running time is indeed an interesting problem and I do not know many possible approaches.
One of simple approaches — as in proving NP-completeness, some problems can be reduced to others. For example we can't solve convex hull faster than
, because if points are placed on circle then determining their order on hull is exactly sorting them radially. If we restrict ourselves to integer coordinates then we can place them on parabola instead of a circle.
Btw, how that statement about shortest path in
can be proved? Btw, to be precise, that 109 is a bit awkward, it would be better to just state that they are integral and we are working in a model when adding/multiplying etc. operations can be performed in a constant time (model assumed in 99% or even more usecases). If we assume that 1 ≤ w(e) ≤ c where c is some constant then problem can be solved in O(mc) — however c is a constant, so O(mc) = O(m) :P.
PRIMES is in P
Although it's not proven to be the best running time, it's the first algorithm to be simultaneously general, polynomial, deterministic, and unconditional that determines if a number is prime or not.
Read more about it on Wikipedia.