С некоторым опозданием публикуем разбор задач прошедшего отборочного тура всесибирской олимпиады.
1. Наносборка
Честно идём по порядку по всем отражениям, которые требуется выполнить, и их для каждой точки. Преобразования можно выполнять следующим образом.
Пусть A — начало вектора, D — собственно вектор, P — обрабатываемая точка.
N = normalize(D.y, - D.x) — единичная нормаль справа.
R = (P - A)·N — знаковое расстояние до прямой сгиба.
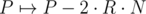 , если rho > 0.
, если rho > 0.
Время: O(N·M). Память: O(N). Автор задачи: Stirpar.
2. Плэйофф
Явно строим получившееся дерево, корнем которого будет команда-победитель. Для каждой команды определяем вершину, где её путь закончился. Команда будет сильнее тех и только тех команд, которые находятся в её поддереве.
При обработке запроса: для каждой из двух команд поднимаемся вверх до корня и если мы на пути встречаем другую команду, значит мы находимся в её поддереве и она сильнее нас.
Время: O(2N·N + Q·N). Память O(2N·N). Автор задачи: package.zaic
3. Неравенства
Неравенства, где оба операнда являются числами, нужно просто проверить. Если есть невыполняющееся, то ответ NO.
Неравенства, где один из операндов является числом, а другой — переменной, нужно превратить в ограничения сверху и снизу для переменных. Итогом является диапазон допустимых значений для каждой переменной.
Остальные неравенства, где оба операнда являются переменными, нужно превратить в ориентированный граф. Вершины графа — переменные, рёбра — неравенства. Неравенства вида (xi ≤ xj) и (xi < xj) дают ребро (xi → xj). Тип неравенства нужно сохранить вместе с ребром.
Для построенного графа нужно построить конденсацию. Если хотя бы в одной компоненте сильной связности есть "строгое" ребро (т.е. такое, которое соответствует строгому неравенству), то ответ NO, поскольку в этом случае есть цикл со строгим ребром. Такой цикл получился из цепочки неравенств, из которой следует xi < xi для некоторой переменной xi, что, очевидно, невыполнимо.
Каждые две переменные из одной компоненты соединены путями в обе стороны. Это значит, что если xi и xj принадлежат одной компоненте, то xi ≤ xj и xj ≤ xi. Значит, xi = xj, т.е. все переменные из одной компоненты обязаны иметь равные значения. Пройдём компоненты в топологическом порядке, и назначим им значения. Каждый раз будем выбирать значение жадно, т.е. минимальное из допустимых. При определении допустимости нужно учесть следующее:
- Ограничения снизу, полученные на шаге 1, для всех переменных из компоненты.
- Все входящие в компоненту рёбра. В силу выбранного порядка они ведут из уже обработанных компонент, а в силу направления — дают ограничения снизу.
Выбранное значение нужно проверить на соответствие ограничениям сверху, полученным на шаге 1, для всех переменных из компоненты. Если хотя бы одно ограничение нарушено, то ответ NO.
Если же удалось назначить значения всем компонентам, то решение системы найдено, и ответ YES.
Время: O(n + k). Память O(n). Автор задачи: xcr
4. Как измерить океан
Для начала перейдём к другим характеристикам для проволоки, а именно к: линейной плотности (вес на единицу длины) и максимальному натяжению (максимальный вес ниже, который держится). Об исходных характеристиках можно забыть. Теперь можно заметить (ключевой момент), что достаточно рассматривать только такие решения, в которых куски проволоки отсортированы снизу вверх по возрастанию максимального натяжения. Доказывается от противного: если какая-то проволока стоит ниже, чем её полагается, можно перенести её наверх, и нигде ничего не порвётся. Если есть виды проволоки с равным макс. натяжением, то достаточно использовать только ту, у которой минимальна линейная плотность. Доказывается очевидно заменой одной проволоки на другую в решении. Если проволока A прочнее проволоки B, но при этом легче, то нет смысла использовать проволоку B: в любом решении можно её спокойно заменять её на проволоку A. Благодаря этому можно дополнительно отфильтровать некоторые виды проволоки. Таким образом, из всего многообразия видов проволоки остаётся набор, упорядоченный строго по возрастанию и по прочности, и по плотности. Если астролябия имеет нулевой вес, то все эти проволоки должны стоять в искомом решении в порядке снизу вверх. В любом случае можно нетрудно доказать (опять же простой заменой), что каждой проволоки следует брать максимально длинный кусок.
На самом деле, большинство вышеописанных утверждений даже не нужно напрямую применять в решении. Достаточно отсортировать проволоки сначала по прочности, потом по линейной плотности. Потом запустить бинарный поиск по ответу (весу астролябии), внутри которого жадно строить проволоку снизу вверх, добавляя максимально возможный кусок проволоки каждого типа.
Время работы: O(N·log(N) + N·log(R / e)). Можно обойтись и без бинарного поиска. Для этого нужно строить проволоку сверху вниз, полагая, что в верхней точке каждого куска достигается максимально возможное натяжение для этого типа проволоки. При этом нужна некоторая аккуратность с проволоками равной прочности. На уровне дна океана надо обрубить проволоку, и повесить снизу астролябию максимально возможного веса. Время: 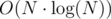
Автор задачи: ruban
5. Спортивное ориентирование
От каждой полянки, на которой нужно отметиться (включая стартовую первую полянку) запускаем алгоритм Дейкстры. После этого достаточно просуммировать полученные минимальные расстояния между соседними полянками-отмечалками. При желании можно запускать Дейкстру только из каждой второй полянки, сэкономив половину времени. Поскольку из каждой полянки можно бежать напрямую в каждую, то граф полный. В таком случае алгоритм Дейкстры без кучи работает за время O(N2) с хорошей константной. Именно его и нужно применять, желательно на матрице смежности. Если использовать Дейкстру с бинарной кучей, то время работы возрастает до 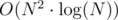 на каждый запуск. Такие решения справедливо не проходили по времени.
на каждый запуск. Такие решения справедливо не проходили по времени.
Время работы: O(K·N2). Память: O(N2). Авторы задачи: Чурина Татьяна и Нестеренко Татьяна.
6. Ставки
Поскольку независимо от результата матча общие затраты одинаковые, то и выигрыш имеет смысл делать одинаковым. Также очевидно, что общий размер ставки значения не имеет, важно лишь соотношение. Значит оптимальные ставки  ,
,  ,
,  . Остаётся только проверить, что выигрыш положительный.
. Остаётся только проверить, что выигрыш положительный.
Так же данная задача вызвала следующие проблемы с точностью и справедливое негодовании со стороны участников:
Поскольку деление даблов даёт погрешность, а нас определять ответ просят точно, то считать здесь надо в целых числах (например, сами числа домножить на 105, а в неравенство домножить на wdl), либо использовать что-нибудь точнее double (например, в той же джаве есть BigDecimal).
Вещественные числа представляются таким образом, что даже числа с небольшим количеством знаков до и после точки будут храниться с погрешностью (выше есть один из самых простых примеров: 0.29), поэтому читать и преобразовывать к int'y их надо аккуратно.
Автор задачи: package.zaic.
7. Муравей на дороге
Сначала проверяем, что ни одна из сторон не может быть полностью перекрыта параболами. Затем:
- Аналитическое решение. Назовем шириной параболы w = sqrt(c / -a) — половину расстояния между точками пересечения параболы с границей дороги. Для северных парабол W = sqrt((1 — C) / A).
Назовем сдвигом s (0 <= s < d) верхней параболы горизонтальное расстояние между ближайшими северными и южными параболами s = abs(B — b); s -= floor(s / d) * d;
Отсечем вначале тривиальные случаи.
а) Параболы покрывают сторону дороги полностью. Если w >= d / 2 или W >= d / 2, то ответ -1.
б) Существует вертикальный путь. Если s >= w + W или d — s >= w + W, то ответ 1
В остальных случая кратчайший путь состоит из отрезка прямой и, возможно, дуг парабол. Понятно, что если в кратчайшем пути есть дуга параболы, то отрезок прямой — касателен к ней.
Итого, возможно три варианта. Выберем из них кратчайший из возможных, проверив их как есть, и с отражением слева направо (s = d — s).
в) Отрезок прямой. Ответ hypot(w + W — s, 1). Возможен при условии, что производная (наклон) отрезка больше производных парабол у краев дороги, т. е. 1 / (w + W — s) >= 2 (-a) w; 1 / (w + W — s) >= 2 A W; Функция hypot — корень из суммы квадратов.
г) Дуга параболы + отрезок прямой. Отрезок должен быть касательным к параболе на конце. Обозначим через q горизонатьное расстояние от вершины параболы до конца отрезка. Получаем уравнение 2 (-a) q = (-a q q + (C — c + A W W)) / (q — (s — W)) Подставим h = s — W; v = C — c + A W W; z = -a q; g = 1 / -a; g z z — 2 h z — v = 0 Дискриминант D = h h + g v Дискриминант будет положительный так ка первый конец отрезка находится снаружи параболы. z = (h + sqrt(D)) / g q = z / (-a) Необходимые условия: 2 z > 2 A W; (т. е. прямая не пересекает параболу) q < w; (т. е. путь по дуге положительный) Ответ arc(-a, q, w) + hypot(A z — h, A z z + v). Функция arc — длина дуги параболы дана ниже.
г') Отрезок прямой + дуга параболы. Аналогично случаю 4, отраженному сверху вниз (a = -A, A = -a, c = 1 — C, C = 1 — c).
д) Дуга параболы + отрезок прямой + дуга другой параболы. Отрезок должен быть касательным к обоим параболам. Обозначим через q горизонтальное расстояние от вершины первой параболы до конца первого отрезка, через Q — от вершиный второй до конца второго. 2 (-a) q = 2 A Q = (-a q q + A Q Q + (C — c)) / (q + Q — s) Подставим v = C — c; z = -a q; g = 1 / -a + 1 / A; g z z — 2 s z — v = 0 Дискриминант D = s s + g v; Если дискриминант отрицательный, то этого пути нет (параболый пересекаются). z = (s + sqrt(D)) / g; (нас интересует только положительное решение) q = z / -a; Q = z / A; Необходимые условия: q <= w && Q <= W; (пути по дугам неотрицательны) Ответ arc(-a, q, w) + hypot(g z — h, g z z + v) + arc(A, Q, W).
Функия arc(a, x0, x1) считает длину дуги параболы от x0 до x1. arc(a, x0, x1) = arc(a, x1) — arc(a, x0) arc(a, x) = h * q / f + f log((h + q) / f), где f = 1 / (4 a) h = x / 2 q = hypot(f, h)
- Численное решение. Рисуем на бумажке параболы, замечаем, что ответом скорее всего будет касательная. При этот если смещать точку на одной из касательных, с которой мы по прямой переходим на другую касательную, то ответ будет монотонно увеличиваться в обе стороны (если, конечно, смещать в разумных пределах, не уходя слишком далеко на противоположную ветвь параболы).
Запускаем тернарник на одной параболе, в который вложен тернарник на другой параболе. Формулу длины дуги параболы либо гуглим полностью, либо гуглим интеграл для расстояния кривой и считаем каким-нибудь Симпсоном. Тут надо заметить, что вложенным тернарником нам надо не минимизировать длину (чтобы не считать каждый раз интеграл), а искать ту точку на второй параболе, когда ближе к краю дороги мы её подвинуть уже не можем (иначе будет пересечение прямой с параболой): в этой точке прямая и будет как можно ближе к касательной.
Автор задачи: ordcoder.
8. Букет
Динамика. Предварительно сортируем цветы так, чтоб один вид шёл подряд.
Параметры: dp[номер последнего обработанного цветка][денег потрачено][брали ли мы уже цветок текущего вида (0 или 1)].
Начальные значения: dp[0][0][*] = 0;
Переходы:
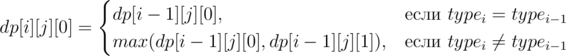
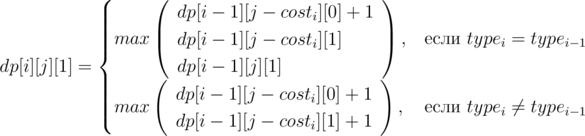
Ответ: max(dp[n][s][0], dp[n][s][1]).
Время: O(N·S). Память: O(S), если хранить только предыдущую и следующую строки динамики. Автор задачи: ruban.
9. Хэш-функция
Научимся обращать операции:
hash = hash + (hash << X) равносильно hash = hash * (1 + (1 << X)), т.е. умножению на 1+(1<<X). Заметим, что это число нечётное и обратный в кольце по модулю 232 для него всегда найдётся, а значит и операцию умножения всегда возможно обратить.
hash = hash ^ (hash >> X) — заметим, что последние Х бит числа до и после операции не изменятся (биты [32 — X, 32) при нумерации бит с нуля). С их помощью мы можем восстановить биты [32 — 2*X; 32 — X) исходного числа. И т.д.
Теперь достаточно по очереди обратить каждую из 5 операций и получить ответ.
Автор задачи: package.zaic.
10. Civilization
Множество городов, которое требуется уничтожить, будем перебирать в порядке уменьшения количества городов (порядок на самом деле не важен, но так проще в реализации).
Теперь у нас есть катапульты и мно-во городов, которые они должны обстрелять. Решать задачу будем с помощью потока. Построим ориентированный граф со следующими долями вершин: катапульты (по вершине на катапульту), клетки (мно-во всех клеток, с которых мы можем обстрелять хотя бы один город), города (по вершине на город).
Из стока проведём ребро к каждой катапульте пропускной способностью 1 (всего C рёбер).
Из каждый катапульты проведём рёбра пропускной способностью 1 в то множество клеток, до которых она может доехать и чтобы при этом осталось 1 ОД на обстрел города. Всего рёбер: C·max(61C, 18N), где 61 — максимальное количество клеток, куда может уехать катапульта, 18 — число клеток, с которых может быть обстрелян город.
Из каждой клетке проведём рёбра пропускной способностью 1 в те городы, которые могут быть обстреляны с этой клетке. 18·N рёбер.
Из каждого города проведём рёбра в сток пропускной способностью, равной здоровью города. Всего N рёбер.
Дополнительно каждую вершину, представляющую клетку, необходимо раздвоить, чтобы через клетку не могло проехать более 1 катапульты. Здесь ещё С·max(61C, 18N) рёбер.
Если на описанном графе пустить поток, то найдётся решение для задачи с нарушением условия, что в одной клетке ход должно закончить не более одной катапульты.
Мне известно 3 способа решить данную проблему:
Во мно-во клеток добавить не только те клетки, с которых можно обстреливать города, но и вообще все клетки, до которых могу доехать катапульты. Добавить ещё один "фиктивный" город, означающий, что катапульты никуда не стреляют. Соединить этот город со стоком ребром пропускной способностью С-(сумма ОЗ по всем городам)
Заметим, что когда возникает ситуация "катапульта приехала стрелять в клетку, откуда другая никуда не уехала", то образуются цепочки вида: катапульта А уехала на место В, В на место С, а С никуда не уехала — их можно разрешить, сказав, что С атакует то, что атаковала В; В никуда не едет и итакаует то, что атаковала А, а А ничего не делает.
Добавим в поток стоимость. Рёбра, ведующие из катапульт в клетки будут иметь следующую стоимость: 0, если ребро ведёт в ту же клетку, где стоит катапульта и 1, если в другую клетку. Всем остальным рёбрам назначим стоимость 0. Тогда ситуация "катапульта приехала на клетку, откуда другая не уехала" разрешится сама за счёт того, что число передвигающихся катапульт минимизируется.
Время: поток любимым алгоритмом на графе с 2·max(61·C, 18·N) + C + N рёбрами и 2 + C + N + 2·max(61·C, 18·N) вершинами. Автор: package.zaic.
11. Стулья
Просто жадность.
Изначально эта задача была частью задачи "букет", но затем была выделена в отдельную задачу с названием "глазет". В связи с похоронной тематикой легенды задачи "глазет", условие пришлось переписать, из-за чего связь "букет"-"глазет" была, в сожалению, утеряна =)
Вермя: 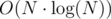 . Память: O(N). Автор задачи: ruban.
. Память: O(N). Автор задачи: ruban.
12. Эрудит
Просто реализация.
Автор задачи: Stirpar.










Спасибо за разбор)
Замечание по поводу 5 — решения с кучей на самом деле проходили. Писал на С++, зашло с плюса.