Hi all,
I'm about to teach AVL trees for a section of 6.006, and while thinking it through, I came up with the following question, which, I strongly suspect, should be well-understood.
Say one wants to maintain a binary search tree with height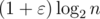 
, where n is the total number of nodes, under insertions. How quickly can one insert? Is time 
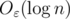per insert possible?
For instance, AVL trees achieve height around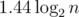 
and red-black trees — 
.
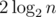What do you think?
Isn't it possible just to generalize AVL trees? E.g. ask for the following property: for each node, consider all of its grand-children of depth k, and require the depth of their subtrees to differ by at most 1. Then for a fixed k, the number of rotations to restore the property is logarithmic (smth like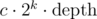
).
As to the limit on depth. Let k = 2; if we greedily construct worst-case for this, the size of smallest tree of depth n is described by fn = fn - 2 + 3fn - 3 + 3, i.e. fn is approximately 1.6717n, and we get the bound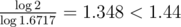
.
If we increase k, it seems that this converges to 1 (e.g., for k = 10 Wolframalpha says that the bound is 1.11, for k = 20 — 1.05). I hope there are no obvious mistakes in my reasoning :)
(I don't understand why your comment has a negative rating.)
Why the number of rotations can be estimated as 2k·depth in general case?
There's O(depth) nodes along the insertion path. For each subtree of such a node there's O(2k) ancestors of grand-children of depth k. We rearrange the ancestors entirely from scratch.
It is more complex than it seems. Suppose k = 2, and children of the left subtree have depths n and n + 1, and for the right subtree — n + 1 and n + 2. Even if we break tree structure at depth k, we cannot re-arrange it so that it is balanced. Even if we break up the n + 2-depth node, it still is not enough. However, if we break up all nodes ≥ n + 1, it seems that it is always possible to re-arrange this.
Though I'm not sure how to easily prove it, I guess the only option is brute force.
Yes, the bound 2k sounds non-trivial. I guess one should start with understanding the case k = 2.
Ok, let's prove this for k = 2. (Disclaimer: not very formally, but IMO convincing enough :) )
Lemma. Suppose one has a sequence of leaves with values 0, 1 of length l ≥ 16,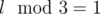
. Then it is always possible to construct (full) quaternary tree on top of these leaves with the following property. Let 
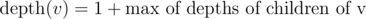, and for leaves, it is the value in the leaf (0 or 1). Then the property is as follows: for each inner node, max(depth of its kids) — min(depth of its kids) is at most 1.
Proof. For l = 16 — brute force, for larger l — try some random sequences and verify that it doesn't find counter-example :) I'm not sure how to properly prove it, but brute force for 16 seems convincing. Note that for l < 16 the statement is not true (in fact, there are lots of counter-examples).
Now back to the original task. Let's eliminate 2nd, 4th, ... layers of the BST and convert it to quaternary tree. Note that we don't require the original property for even layers as the result, but depth guarantees still stand. Let's add a new node, and list all the inner nodes where the property is broken (O(depth) of them). Let's go from bottom to top and restore the property applying the lemma.
Suppose we have node v with broken property. Let's build the following auxiliary tree (with size limited by a small constant — say 256). Take v, its kids, and their kids. Then look at the m := min(depth of the nodes in the new tree), and take more kids until depths of all the leaves are ≤ m. We'll get a tree where all leaves have depth in the original tree either m or m - 1. Now let's apply the lemma: it immediately gives us the new structure of this (constant-size) part of the tree.
Is it convincing enough? :) I think this strongly indicates that the same works for bigger k. Though proving this rigorously might be difficult.