In the very beginning of this post I would like to thank everyone who contributed to make this contest happen — both onsite and online versions. For many of us it was practically the first contest we really took part in preparing of — we all loved working on it and hope you liked it too.
I would also like to mention that 2864 teams (about 4k people!) registered to this contest, 1025 actually took part in it, 637 managed to solve at least one problem and there were 4 teams that solved all the problems before contest ended. Congratulations to everybody! Ok, so here is top 10 of Codeforces version of Bubble cup:
| 1 | tourist |
| 2 | Nizhny Novgorod SU: mike_live, vepifanov |
| 3 | SPb ITMO University 1: antonkov, enot110, subscriber |
| 4 | Dreadnought: TankEngineer, rowdark, BaconLi |
| 5 | nedrharmsw: AntiForest, rnsiehemt, JoeyWheeler |
| 6 | Orz!: zcz, KFDong, ExfJoe |
| 7 | -XraY- |
| 8 | Saratov SU Daemons: danilka.pro, Edvard, kuviman |
| 9 | Omogen Heap: Gullesnuffs, simonlindholm |
| 10 | Bsuir_power: andrew.volchek, teleport |
All of them will get T-shirst. But apart from them, as we promised, there will be 10 T-shirts more sent to randomly chosen teams, here they are:
22 HellKitsune
40 tmt514
77 Saratov SU 3: Perforator, Oleg_Smirnov, Roms
82 Greed_for_Speed: m17, aditya_kakarot, shiva_r31
For those who are interested here is a link to results of onsite competition.
Since editorial is pretty big I think it is more reasonable to share link to file here than posting it all here.











".docx" T_T ..........
There is a joke on UW that one particular of our professors has solved TSP problem, but he is ashamed to publish it, because he has written solution in .docx format
thx for comment, changed to pdf-file
When I read the first entry about competition, I read it wrong, so instead of "10 t-shirts will be handed out randomly to other participants of the top 100", I read something close to random 10 teams from top 100 will get t-shirts.
Later on, of course I realize my mistake, but now I'm very curious about implementation of this t-shirt algorithm. As far as I concerned, it's really hard to give 10 t-shirts to a random teams, that sum of team members will be equal to 10 and also satisfy the uniform distribution (of course you didn't said you will give t-shirts based on uniform distribution)
Could you reveal some information on your random generator?
algo randomly picks a team and if we have enough T-shirts left we take that team, else trying to pick once more.
H. Bots. It can be simply shown that the number of possible solutions is equal to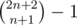 . So it is needed to find
. So it is needed to find
I knew about this solution, but i didn't know how to prove it.
Answer is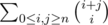 , which is basically "square" from Pascal's triangle. To simplify this we can use "golf club theorem" two times which unfortunately I'm unable to find in Internet. It says
, which is basically "square" from Pascal's triangle. To simplify this we can use "golf club theorem" two times which unfortunately I'm unable to find in Internet. It says 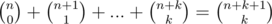 . After marking involved summands you will understand why it's called golf club theorem :P.
. After marking involved summands you will understand why it's called golf club theorem :P.
I like other name more — Christmas Stocking Theorem :)
It's also known as the "hockey stick theorem".
Also known as Chu Shih-Chieh’s Identity, at least in my lecture notes :)
Or just precalculate first few numbers and search for the producing formula: https://oeis.org/search?q=1%2C5%2C19%2C69 )))
It cannot be proof of statement.
good problems! But most chinese students can't use dropbox, sad...
why solving it with HLD? LCA here is much more obvious. And much easier to implement
Yes, you are right. But for me, when dealing with path in tree , the first idea came into my mind is HLD.
Rehosted, in case it's useful: http://www.pdf-archive.com/2015/09/07/editorial/editorial.pdf
Thanks.It's very helpful.
In problem H, can someone explain why most of the solutions include C(i, N) * C(i, N)?
H. Bots. What does "Number_of_duplicating_vertices_from_level" stands for? Is it number of vertices on level
ieach of which will produce two vertices on leveli+1? DoesC(i,N)stands fori choose N?yes
ibra, thanks, it must be I don't understand here something. If I look at trie for
N=3there is 6 vertices on level 3 that produce duplicates. But according to PD definitionPD(3) = 2 * C(3,3) = 2. What I missed?thanks for comment, it is a typo.
PD is number of vertices that do not duplicate (because they already spent all 0s or all 1s),
and of course then, Count[i+1] = PD(i) + (Count[i]-PD(i))*2
will correct it now
In the editorial for problem F, when it says "If x_turn is shining, then pos' is shining as well, so we could have finished our turn there.", isn't that only true if x_closer2 <= pos'?
Also, how can we justify that it is optimal to stay at an endpoint when x_turn is not shining?
Sorry if not clear enough, the only sentence about x_turn shining is "If x_turn is shining, then pos′ is shining as well, so we could have finished our turn there.". Other part of the paragraph is about x_turn not shining.
And statement "If x_turn is shining, then pos′ is shining as well, so we could have finished our turn there." is always true. Take a look at the picture above that sentence. pos' and pos'' are the closest light-up endpoints to the x_turn, so the smallest interval of shining bulbs is at least [pos', pos'']. Rationale: if x_turn is shining and it is not the endpoint then one endpoint is left other endpoint is right...
Right, I didn't notice that. Thanks for the explanation.
For Tablecity I made a smaller version where you can do it yourself, I made it on a webpage, you can download it here
Was the solution file down? I can't open the Dropbox link. Can anyone upload a new one?
I can't open the Dropbox link either.I need the solutions too!!!
editorial is deleted , could you restore