Коварные стрелочки

Типичный посетитель сайта codeforces.com, наверное, знает, как искать минимальное (или даже максимальное) остовное дерево (а то и остовный лес). Умеет писать алгоритм Прима, алгоритм Крускала. Кое-кто может быть даже в курсе, что всё это частные случаи алгоритма Борувки, который в 1926-м году рассказывал, как оптимально электрифицировать Моравию (регион Чехии). Вот только правильно работают эти алгоритмы исключительно для неориентированных графов .

Напомню задачу. Дан взвешенный граф G = (V, E, γ) ( V — множество вершин, E — множество рёбер или дуг, γ — функция веса на рёбрах или дугах). Требуется найти подмножество рёбер (дуг) S ⊆ E, такое, что:

• В графе (V, S) не будет циклов (в ориентированном случае есть дополнительное ограничение: в каждую вершину должно входить не более одной дуги из S).
• Среди таких максимальное по включению: нельзя добавить ещё одно ребро (дугу), чтобы не сломалось предыдущее ограничение. Замечу, что из этого следует глобальная максимальность по количеству рёбер (дуг).
• Среди таких минимальное по весу: γ(S) = γ(e) следует минимизировать.

В неориентированном графе достаточно было (алгоритм Крускала) брать рёбра в порядке увеличения веса, добавлять в граф, если они не образуют цикл, иначе выкидывать. К сожалению, в случае ориентированного графа нас ждёт неприятный сюрприз.

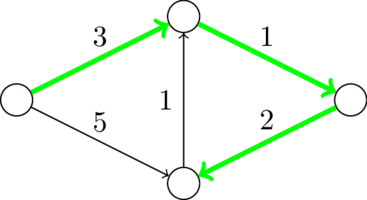
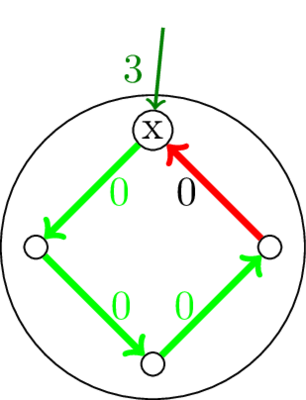
На картинке выше минимальное остовное дерево выделено и имеет вес 6, но после добавления двух дуг веса 1 такое становится недостижимо. Что же делать?

Хитрые китайцы

Как быть с ориентированными графами миру рассказали в 1965-м году два китайца: Чу Йонджин и Лю Цзенхонг. Независимо от них примерно в то же время (публикация в 1967-м году) аналогичный алгоритм разработал Джек Эдмондс. Задача-то не шибко сложная. Тоже жадность, просто чуть более хитрая, чем для неориентированного графа.

Для начала немного определимся с задачей. Есть вариант, который я описывал в «Коварных стрелочках», когда ответ — лес корневых деревьев (то, что называют branching, «ветвление»). А есть вариант с выделенным корнем, тогда требуется построить подвешенное за этот корень дерево минимального веса (соответственно, arborescence, «древовидное образование»). Первый вариант легко сводится ко второму: добавим в граф фиктивный корень и нарисуем по дуге бесконечного веса в каждую вершину из этого корня. Бесконечность, как обычно, следует подбирать аккуратно, чтобы из неё можно было что-нибудь повычитать, и после этого ещё посравнивать.

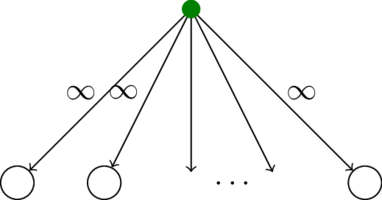
Сведение в обратную сторону ещё проще: выкинем дуги, идущие в корень (их нет в правильном ответе), после этого если существует arborescence, то оптимальный branching является и оптимальным arborescence тоже. Предлагаю решить задачу arborescence, потому что тогда встретится меньше неприятных случаев.

Алгоритм

Почему бы для какой-то вершины не посмотреть на все входящие в неё дуги. Если мы добавим (или вычтем) какое-нибудь число к весу этих дуг, то задача не изменится: в эту вершину в ответе входит ровно одна дуга и вес ответа изменится ровно на это число. Вычтем из входящих в вершину дуг вес минимальной из них.

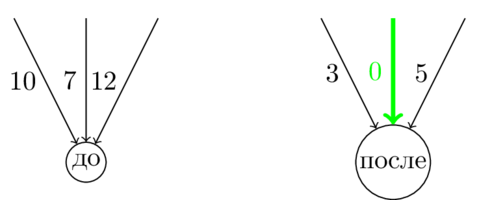
Теперь в вершину приходит хотя бы одна дуга веса ноль, а веса остальных дуг неотрицательны. Конечно же, эту нулевую дугу хочется добавить к ответу. Что же выйдет, если провернуть эту операцию с каждой (кроме корня) вершиной графа?

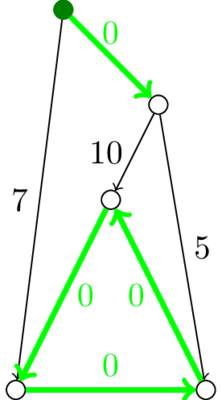
Графов вида «в каждую вершину приходит одна дуга» не так уж и много. И, напомню, в одну из вершин входит ноль дуг: корень дерева. Может реализоваться два варианта: скучный и не очень. В скучном варианте все вершины нулевыми дугами соберутся в дерево, это и будет очевидным образом правильный ответ. Но могут появиться и циклы.

Описание алгоритма на викиконспектах предлагает в таком случае сконденсировать граф по этим циклам (или даже по компонентам сильной связности, если брать все дуги веса ноль, а не только по одной для каждой вершины) и повторить ещё раз. Оригинальную статью Чу и Лю я, увы, не читал, но почему-то мне кажется, что явное конденсирование графа — изобретение итмошников, а авторы алгоритма обходились без него (если и делали, то неявно).

Здесь, кстати, важно, что мы вычитали веса дуг у вершины, а не просто взяли минимальную. Смысл цикла из нулевых дуг в том, что можно прийти в любую вершину цикла, и это автоматически даст нам путь до всех остальных вершин цикла. То есть, если мы придём в вершину x, то просто заменим нулевую дугу, ведущую в x по циклу, на дугу извне. За эту операцию нам придётся заплатить разностью весов дуг, поэтому, чтобы на следующей итерации вес дуги означал цену его добавления, приведём вычитаемое к нулю.

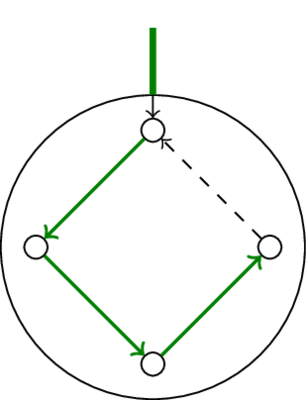
Восстановление ответа

Не очень хитрое, если явно сжимать граф (и хранить конденсации с каждого из сжатий). Надо на каждом цикле понять, какую дугу нужно выкинуть. Подсказка: ту, которая приходит в вершину, посещённую дугой из верхнего уровня.

Если сжимать не простые циклы, а компоненты сильной связности, то восстанавливать будет чуть сложнее. Придётся написать обход в глубину, который по компоненте и первой посещённой вершине выдаст пути до всех остальных.

Время работы

В худшем случае может оказаться, что на каждом шаге сконденсируется всего один цикл длины два, тогда достигается время работы Θ(n·m), где n — количество вершин в графе, а m — количество дуг.

Однако, если подойти к задаче чуть аккуратнее, то можно уложиться в O(m·log n + n²), а то и в O(m·log n) (или даже в min (m·log n, m + n²), но это останется читателю в качестве упражнения).

Тарьян смог, значит и мы справимся

Нам понадобится лом, разобранный газотурбинный двигатель и парочка структур данных. Роберт Тарьян же ещё в 1977-м году написал статью Finding Optimum Branchings

Общая идея

Конечно же, явно перестраивать граф после каждого сжатия цикла никто не хочет. Просто надо работать не с вершинами, а с их группами (дальше я буду называть их «компонентами»). Хранить их можно в самой обычной системе непересекающихся множеств. Удобно отнести в отдельную компоненту вершины, для которых уже нашли ответ («нулевой» путь из корня), вместе с самим корнем.

Дальше можно воспользоваться тем, что базовый алгоритм — жадность. В каком порядке брать нулевые дуги — неважно, корректность от этого не меняется, можно делать как удобнее. Лично мне удобнее взять вершину, и пойти от неё в сторону корня. То есть, найти минимальную входящую дугу, вычесть, пройти по нулю, взять минимальную дугу, вычесть, пройти, и так продолжать.

Такой поход может закончится одним из двух вариантом. Первый: пройдя по очередной дуге, попадём в компоненту корня (то есть, в сам корень либо в вершину, до которой уже есть путь из корня). Он просто означает что для исходной вершины (и для всех вершин на пути) ответ тоже нашёлся, осталось его восстановить и объединить компоненты с корневой.

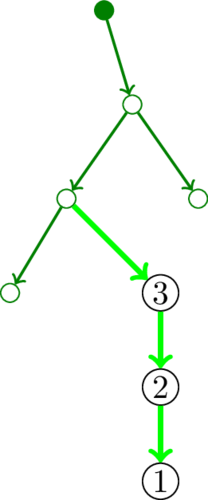
Другой вариант расстроит фанатов игры «змейка», зато обрадует древних греков буквой ρ. Пройдя по дуге, попадём в вершину на пути, которую мы не так давно посещали. Здравствуй, цикл.

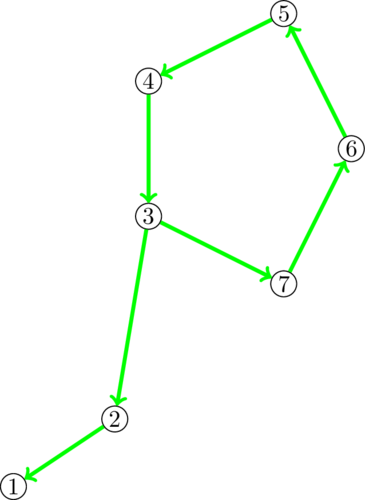
Самое время этот цикл сжать (то есть, объединить его компоненты в одну — помним, что сжатие исключительно неявное). Это вполне можно сделать за размер цикла (пройдясь по нему ещё раз), после чего продолжить поход, но уже обрабатывая бывший цикл как одну компоненту. Компонент в графе стало меньше, значит рано или поздно, сжав много-много циклов, доберёмся до корня.

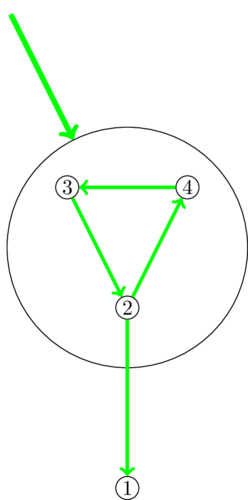
Пройдёмся по всем вершинам графа и, встретив ещё не обработанную, приведём её описанным выше способом в корень (возможно, по ходу обработаем не только её, но ещё несколько вершин).

Реализация

Но для таких фокусов понадобится вторая структура данных: выковыривать минимальную входящую дугу из целой компоненты надо быстро. В структуре следует хранить множество входящих дуг (альтернативный вариант: заранее отсортировать входящие дуги для каждой вершины и хранить множество вершин). Мы хотим от структуры данных следующее:

• взять минимум
• удалить минимум (в альтернативном варианте — взять следующую дугу в списке вершины, а в структуре данных сделать изменение одного значения)
• добавить число ко всем весам
• объединить две структуры в одну

Операция «удалить минимум» нужна по следующей причине. «Ленивое» сжатие графа означает, что удалять петли (дуги внутри компоненты) никто не собирается. Поэтому операция «взять минимальную входящую в компоненту дугу» вполне может вернуть дугу, исходящую из той же компоненты. В таком случае надо всего лишь удалить эту дугу из структуры данных (каждую дугу графа придётся удалять не более одного раза, время работы не пострадало) и попробовать взять минимум ещё раз.

Вариантов структуры данных для такого дела довольно много. Декартово дерево по неявному ключу со случайным приоритетом, посчитанным минимумом на поддеревьях и операцией на отрезке. Splay-деревья при правильном подходе. Какие-нибудь сливаемые кучи. Или хотя бы пара из std::set и сдвига: подход «при объединении взять элементы из меньшего и по одному добавить в большее» даёт перекидывание каждого элемента не более 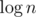раз, правда, этот логарифм вылезет лишний раз в асимптотике времени работы: .

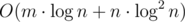Подробный разбор времени работы я тоже оставлю читателю, интересный остался один момент.

Восстановление ответа

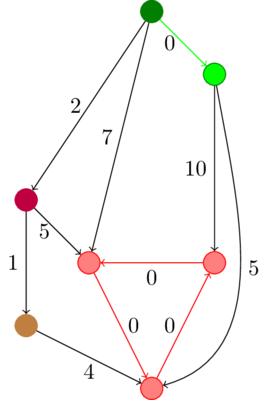
Требуется понять, какие из дуг, взятых по ходу алгоритма, надо оставить, а какие — удалить, чтобы разомкнуть циклы. Для этого нужно помнить, как мы сжимали граф, иначе информации не хватит. На картинке два одинаковых графа, но если сначала был сжат цикл b → c → d, то вместе с db следует выкинуть дугу ed, а если цикл b → e → d, то дугу cd.

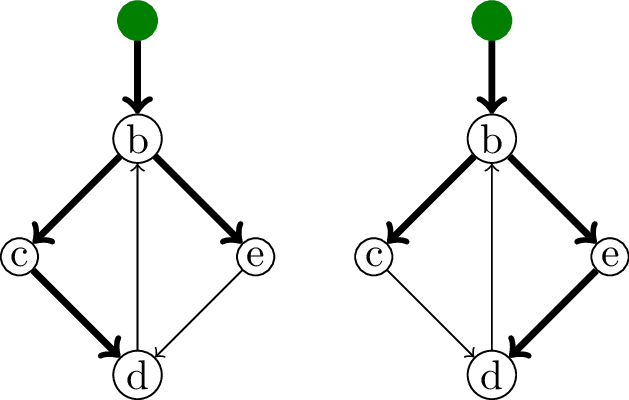
Более того, дуги cd и ed могли иметь различный вес до вычитания минимумов, потому что обнулялись на разных шагах.

Это означает, что для восстановления ответа придётся честно спускаться вниз по компонентам. Для каждой (появлявшейся по ходу работы алгоритма) компоненты запомним, из каких компонент нижнего уровня она состоит, разворачивать будем рекурсивно. А вот если мы решили какую дугу взять, то следует пометить достигнутыми все компоненты, в которые входит эта дуга. Да, их может быть много (если дуга на внешнем уровне входит в вершину большой глубины), но каждая компонента окажется достигнутой ровно один раз.

Это можно легко сделать, если заранее для каждой компоненты сохранить ссылку на внешнюю следующего уровня. Тогда, решив взять в ответ какую-нибудь дугу, нужно всего лишь подняться от одной вершины в компоненты всё более высокого уровня и пометить их как посещённые. Рекомендую пронумеровать все компоненты, которые появляются по ходу работы, целыми числами.

Спасибо за внимание

Для тех, кто дочитал до конца, подарок в виде моего кода на эту тему.