http://www.codechef.com/COOK53/problems/RRPLAYER
This is the problem link. I have one doubt here.
Although I agree with the states mentioned in the editorial. But, when I was trying to solve it on my own. I create the states as F(i,j) meaning i songs have not been played even once and j songs have been played atleast once. With this, I can have the following recurrence relations
These are some base cases.
f(0,i) = 0.0 //all songs have been played once. f(i,0) = [1 + f(n-1,1)]/i
Now, lets derive for other (i,j)
f(i,j) = [1 + f(i,j)]/j + [1 + f(i-1,j)]/i
f(i,j) = 1/i + 1/j + f(i,j)/j + f(i-1,j)/i
f(i,j)[1-1/j] = [i + j + j*f(i-1,j)]/(i*j)
f(i,j)*(j-1)/j = [i + j + j*f(i-1,j)]/(i*j)
Cancelling j from both sides on denominator
f(i,j) = [i + j + j*f(i-1,j)]/(i*(j-1)) //final recurrence relation
But if you see, this becomes undefined for f(i,1) because in denominator there is a term for (j-1). What am I missing here?
This is a well known problem called the Coupon collector's problem. For n songs, the answer is n·Hn where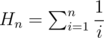
. The intuition lies in defining the random variable E(i) which denotes the expected songs needed to be listened to get a unique song if you have already heard i songs. Thus, E(0) = 1, as any song you listen to in the beginning will be unique. For E(1), E(2) and so on, the probability of getting a unique song is a geometric random variable with probability of success 
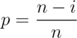. Thus the expected value is 
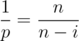. Sum these up for all i's and you get the answer. (by linearity of expectation)
Thats perfectly okay. :) But, what if one does not know that?
I am looking for some mistake in my recurrence mentioned in my post. I will be really glad if you would help me out there.
Thanks for your reply. :)
Anyone for help?