Hello everybody, Could somebody provide me with a good tutorial for suffix array data structure?
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3857 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 161 |
| 3 | Qingyu | 160 |
| 4 | Dominater069 | 159 |
| 5 | atcoder_official | 157 |
| 6 | adamant | 153 |
| 7 | Um_nik | 152 |
| 8 | djm03178 | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/28/2025 10:55:15 (h2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Why not Codechef?
Thanks, actually I've read it before but I need better resources
What do you mean by better resources?
I felt that it is not clear enough for me
Did you learn this data structure from this tutorial ?
No, I don't know suffix array yet, it's still on my TODO list :D But I thought the explanation from kuruma would pretty clear and detailed.
What is suffix array data structure. Can someone explain generally in several words.
It is array p for string s such that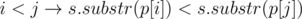 .
.
Simply put, suffix array is a sorted array of suffixes of a given string.
Okay, think what you need for a suffix array in better than O(N2) time. You want to sort suffixes in alphabetical order. Sorting is simple,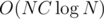 , where comparing 2 suffixes takes O(C) time. The main point is optimising C.
, where comparing 2 suffixes takes O(C) time. The main point is optimising C.
Comparing 2 suffixes = finding their longest common prefix (LCP), then you can just compare the characters that follow after that LCP. The LCP can be found using binary search, where you only need to check if 2 substrings are equal. That can be done by comparing their hashes, and the hash of any substring can be computed in O(1) time with O(N) preprocessing. This way,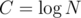 and it's often sufficient (possibly with trying to squeeze into the time limit).
and it's often sufficient (possibly with trying to squeeze into the time limit).
There's a better approach that makes suffix array construction . The previous approach used a custom comparison operator and any suitable sort(). This one uses radix sort (at least I think that's what it's called): you sort the strings by first character, then by the first 2 characters, by the first 4, 8... up to a sufficient power of 2. In step k, you store strings with the same first 2k characters in buckets, which are split into smaller buckets in the next step using the ordering by these 2k characters.
. The previous approach used a custom comparison operator and any suitable sort(). This one uses radix sort (at least I think that's what it's called): you sort the strings by first character, then by the first 2 characters, by the first 4, 8... up to a sufficient power of 2. In step k, you store strings with the same first 2k characters in buckets, which are split into smaller buckets in the next step using the ordering by these 2k characters.
How to do that? Number the buckets in increasing alphabetical order of the 2k characters. Take empty meta-buckets numbered in the same way. Traverse the suffixes in order of non-decreasing bucket number; if prefix s[i..N] is in bucket b[i], then put s[i..N] to the meta-bucket numbered b[i + 2k] — you're sorting them by the next 2k characters, basically. Then traverse the suffixes in non-decreasing order of meta-bucket number and put them back in the original buckets in that order. Tada, they're now sorted by the first 2k + 1 characters! All that's left is splitting the original buckets further, which can be done simply — just when 2 successive prefixes went in a different meta-bucket, then they'll be in different buckets afterwards.
The reason is that when 2 prefixes were in different buckets before, they will be in different buckets (and in the same order) afterwards, and if they were in the same bucket before and in different ones afterwards, then the smaller one will go into a smaller meta-bucket. This is just array juggling in O(N) per step, and you can stop when 2k > N, so the total time is really .
.
Suffix arrays can also be constructed in O(N), but why?
Thanks so mush Xellos :)
Can you please provide the O(n logn) code using radix sort if you have it in your library?
Don't you know to use google search ?
http://web.stanford.edu/class/cs97si/suffix-array.pdf
It is nice blog and you can read this.
https://cp-algorithms.com/string/suffix-array.html