Блог пользователя speedster

prove this.
Автор speedster, история, 10 лет назад, По-английски

How can we prove this : no of unique outputs to (i*j)%k where i can be any number j and k are known is k/__gcd(k,j);

  • Проголосовать: нравится
  • -1
  • Проголосовать: не нравится

»
10 лет назад, # |
← Rev. 2   Проголосовать: нравится +8 Проголосовать: не нравится

You need to find for which a there exists a solution to ij ≡ a (mod k) where i is a variable. Obviously if (k, j) = 1 then j has an inverse mod j so for any a < k there exists an unique solution.

Now suppose (k, j) = d! = 1, then your equation becomes equivalent to finding an l such that ij = lk + a or ij + ( - l)k = a. A pair i, l exists if and only if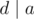 , so a = dx where x has some random value. Now you have d * x < k so x < k / d, so x can range from 0 to k / d - 1, so there are exactly k / d variables for which there exists a solution.

→ Ответить