There are 3 numbers: T, N, M. 1 ≤ T, M ≤ 109, 1 ≤ N ≤ 1018 .
What is asked in the problem is to compute 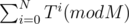 . Obviously, O(N) or O(M) solutions wouldn't work because of 1 second time limit. What can I do?
. Obviously, O(N) or O(M) solutions wouldn't work because of 1 second time limit. What can I do?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 153 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
There are 3 numbers: T, N, M. 1 ≤ T, M ≤ 109, 1 ≤ N ≤ 1018 .
What is asked in the problem is to compute 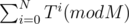 . Obviously, O(N) or O(M) solutions wouldn't work because of 1 second time limit. What can I do?
. Obviously, O(N) or O(M) solutions wouldn't work because of 1 second time limit. What can I do?
| Name |
|---|



You should in parallel count Tn and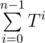 , like in binary exponentiation. It's a small exercise to realize how it should work :)
, like in binary exponentiation. It's a small exercise to realize how it should work :)
I just saw this page. By using that formula I can solve it in O(logN), but I couldn't understand what you meant. Can you elaborate a little?
The main idea is that 1 + T + ... + T2n - 1 = (1 + Tn)·(1 + T + ... + Tn - 1). So, knowing the values of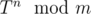 and
and 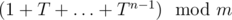 , we can calculate the desired value. To find sum up to 2n, simply take 1 + T·(1 + T + ... + T2n - 1). So, the algorithm is quite the same as binary exponentiation, but you should keep two values during each step.
, we can calculate the desired value. To find sum up to 2n, simply take 1 + T·(1 + T + ... + T2n - 1). So, the algorithm is quite the same as binary exponentiation, but you should keep two values during each step.
I understand it now, thanks for a great explanation.
T1 + ... + T2N = (TN + 1)(T1 + ... + TN)
shouldn't it be (T ^ (N + 1) + 1)( T ^ 1 + ... + T ^ n)? UPD: i was wrong
nope, notice that there is no T^2n+1 in the summation.
Sorry, I didn't notice that there T^1, not T^0
me neither
A more straightforward solution is based on the sum of geometric series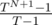 : calculate TN + 1 - 1 modulo (T - 1)M with binary exponentiation and divide the remainder by T - 1.
: calculate TN + 1 - 1 modulo (T - 1)M with binary exponentiation and divide the remainder by T - 1.
You could not do it if gcd(T - 1, M) ≠ 1. There is a way to avoid this, counting which powers of prime divisors of M numbers TN + 1 - 1 and T - 1 are divisible by, but it's too complicated.
I think it will work. Note that I calculate the numerator modulo (T-1)M, not modulo M.
Oh, sorry, you are right. But if T and M were up to 1018 (maybe this information would be useful for the topicstarter), there would be problems, which we can avoid in the first solution, using binary multiplication.
And in this solution we should also use binary multiplication, since T·M could be up to 1018. So the complexity is a little worse.
I also thought about it a moment ago, but then I've realized problem states that T - 1 and M are not necessarily relatively prime.
Assume that TN + 1 - 1 = k(T - 1)M + r, r is the remainder modulo (T - 1)M. Because T - 1 divides left-hand side, it must divide the right-hand side: r = (T - 1)r'. We obtain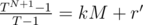 , i.e. r' is the remainder modulo M.
, i.e. r' is the remainder modulo M.
Okay, thanks!
do we need bignum? (T — 1)M can be up to 1e18 — 1e9
Yeah, Kostroma mentioned above that this would require a 'Russian peasant' modular multiplication.
thanks for the info
I read wikipedia's Russian peasant multipication so the overall complexity would be O(lg^2 n) right?
slycelote was faster :(
f(n) = f(n - 1) * t + 1
But this is O(N). It would get TLE since N can be up to 1018
You can use matrix powers to solve this recurrence relation.
Didn't you know "Matrix Exponential"?
Oops, I've missed that. Thank you!