cgy4ever's blog

Short Editorial of SRM 658 Div1
By cgy4ever, 10 years ago, In English

Short Editorial of SRM 658 Div1

Reference Code:

Div2-Easy: http://ideone.com/O7yBlI

Div2-Medium: http://ideone.com/cazTBB

Div2-Hard: http://ideone.com/rxEUcR

Div1-Easy: http://ideone.com/JLuDVM

Div1-Medium: http://ideone.com/7FEz1K

Div1-Hard: http://ideone.com/clL4Rk

Editorial:

Div1-Easy:

The key is that: Any tree is a bipartite graph!

That means, if two nodes are in the same part, then the distance between them is an even number, otherwise it is an odd number.

Assume the 0-th node is in first part, then we can know which part each node belong to by looking at x[0][i] : if x[0][i] is 'E' then i-th node should be in the first part, otherwise it should be in the second part.

There are few things to check:

  1. x[0][0] should be 'E'.
  2. there should be at least one node in both part, i.e. there should exist i such that x[0][i] = 'O'.

And then we can check if for all i,j: x[i][j] = (i-th node and j-th node in the same part ? 'E' : 'O'), if not, there is no solution.

Otherwise we can build any spaning tree of this complete bipartite graph, for example we can use this:

1 - 1
1 - 2
1 - .
1 - m
2 - 1
3 - 1
. - 1
n - 1

Div1-Medium:

Suppose for the i-th SCV: it received x9[i] times attack as the first target (so damage is 9), x3[i] times attack as second target, and x1[i] times attack as third target.

If we totally attack t times, then these conditions are necessary:

  1. For each i, x9[i] * 9 + x3[i] * 3 + x1[i] * 1 ≥ x[i]: this means the i-th SCV must received enough damage to be destroyed.
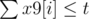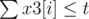  2. , and 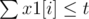: this means we can't have more then t 'attack as first/second/third target'.
  3. For each i, x9[i] + x3[i] + x1[i] ≤ t: this is because one SCV can not be attacked more than t times totally.

What's amazing is that these 3 conditions are sufficient. I will skill the proof here (In fact I don't have a nice one -- it is ordinary case analysis, if you know a better one then please tell us, thanks!)

Then it becomes easy: First we do the binary search for the answer. Then we can do DP. DP[cur][i][j] := if we use totally i times 'attack as first target' and j times 'attack as second target' to kill all first cur SCV, then what's the minimal number of 'attack as third target' can be?

Div1-Hard:

This task ask the following thing: given a bipartite graph with n nodes in both part, find b: a subset of boys such that: 1. the girl they loves, or say, the neighborhoods of b: |neig(b)| = |b|, that means, any of them don't love girls that is not in this matching. 2. There is a matching of these |b| boys with these |b| girls.

Formula like |neig(b)| = |b| give us a hint for Hall's marriage theorem: Suppose the maximal matching of this bipartite graph is n — d, then we can find b, a subset of boys, such that |b| — |neig(b)| = d. (We can use maxflow algorithm to find such set, by getting the minimal cut)

And then we can do max matching for these |b| boys and |neig(b)| girls, it will give you a valid answer (so we never return {-1}). Why? You can prove the maximal matching of this subgraph is |neig(b)|, once again, by Hall's marriage theorem.

  • Vote: I like it
  • +67
  • Vote: I do not like it

»
10 years ago, # |
  Vote: I like it +9 Vote: I do not like it

what was the hack on Div2 easy ??

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it 
    abcab
abc
    → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    something like {9, 8, 6}

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      many tried to solve it using greedy that's

      (9, 8, 6) -> (0, 5, 5) -> (0, 0, 2) -> (0, 0, 0) => 3

      (9, 8, 6) -> (0, 7, 3) -> (0, 0, 0) => 2

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      he ask div2 easy, not medium

      → Reply
      • »
        »
        »
        »
        10 years ago, # ^ |
          Vote: I like it -8 Vote: I do not like it

        oops, i don't know how but "easy" seemed "500" to me! :P i'm not drunk i swear

        → Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    [Hint]

    Do you know how to solve this problem: Given n string, connect all of them in some order to get a long string, what's the lexicographic smallest one you can get?

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you solve this problem with this sorting algorithm: If xy < yx then x before y in final order otherwise y before x. When you sort array you easily print s[1]+s[2]...+s [n]

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      LCM

      → Reply
    • »
      »
      »
      10 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I took the smallest string and repeted it until it's lenght is not less than the other, but I was hacked :/

      → Reply
  • »
    »
    10 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Fairly easy solution will be to repeat both strings and make them of length = lcm(length of string s, length of string t). Then simply compare the two resulting strings.

    Got my solution accepted this way :)

    → Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +44 Vote: I do not like it

When I see the Fox Ciel and StarCraft, I guess the problems are from you. :)

→ Reply
»
10 years ago, # |
  Vote: I like it +8 Vote: I do not like it

I can't understand the "<=" in condition 1 of Div1-Median.

"For each i, x9[i] * 9 + x3[i] * 3 + x1[i] * 1 ≤ x[i]: this means the i-th SCV must received enough damage to be destroyed."

Is this right? It would not be >=?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Yes it should be >= ("\geq"), somehow I thought it is 'larger or equal' and typed '\leq'..

    → Reply
»
10 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Can anyone explain Div-I 500 in a more detailed fashion?

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

div2 Hard ?

→ Reply
»
10 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Question about Medium in Div2,if S sum of given vector.Can we find answer according to S?

→ Reply
»
10 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Wow div2 Easy in 1 line, that is way more efficient that mine, like, 65 lines more efficient.

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +16 Vote: I do not like it

About Div1-Medium proof, I think what's left is to show, that if you have a matrix with non-negative integers, with sum in each column and each row limited by t, then we can represent it by a sum of t one-zero matrices, each of them having at most one 1 in each column/row. This is the same as proving, that bipartite graph with multiedges can be edge-colored using max-deg colors. And I think, that is a known fact.

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

anyone from div2 solved div2 easy having the same solution with provided solution in this editorial? i feel bad after seeing the solution :'(, how can i miss that easy approach :'(

→ Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In Div-1 medium doesn't condition 3 imply condition 2?

→ Reply
»
10 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

I did a rather brute-force solution for Div1-850 and got accepted (in practice mode).

My solution goes like this. First, start with the full bipartite graph of all relationships, then...

1) Run max-flow.

2) Find all nodes on the left part that are connected to nodes on the right part that still have capacity. Remove those nodes from the left part.

3) If we didn't find any nodes in step 2, print the matching, otherwise, go back to step 1.

I thought it would get TLE, but it actually got accepted.

→ Reply
»
10 years ago, # |
  Vote: I like it +21 Vote: I do not like it

Can anybody say something about corectness of my code for Div1-650: http://ideone.com/mHcJeB ? I didn't have any reasonable ideas during coding phase, so I went for I-thought-heuristic solution, which may turn out to be correct, but I don't know. I got minor bugs during coding phase, but when I debugged it after contest it got accepted on system test, but I'm still dubious about its corectness.

My idea goes as follows:
We will be using that fact that those 3 conditions are sufficient. Binary search on answer. Then we will proceed with modified greedy. Greedy without modification goes like this "take guy with highest hp and shoot him with strongest remaining shot". It is clearly wrong since some guys with less remaining hp cannot take more than some number of shots and we need to use strong shots on them. So before performing each phase of that greedy (it is divided into three phases of shooting with 9, 3, 1) we will shot all guys with the least number of shots of that value that he has to be shot with. And then proceed with greedy.

If that's correct then its complexity is definitely better than those of model solution, because it runs in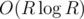 , where R is result, or sth like that, whereas model solution runs in O(R4) or sth (that inner binary search in my code is very stupid, it can be replaced with one formula, but I was too lazy to wirte it down :P). And if it's correct then I think that proof will take advantage of fact that 1 divides 3 and 3 divides 9.

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +56 Vote: I do not like it

    Too lazy to write stress test? :)

    {46, 53, 28, 3}
    Answer is 10, while your solution returns 11.

    → Reply
    • »
      »
      »
      10 years ago, # ^ |
      ← Rev. 2   Vote: I like it +18 Vote: I do not like it

      Thanks :D. I think that sometimes skill of writing good heuristics is also valuable xD.

      → Reply
»
10 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can you explain step with maxflow in div1-hard?

→ Reply
  • »
    »
    10 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    You make this kind of graph: for each i: S -> L[i] with cap = 1, R[i] -> T with cap = 1, and add edges like L[i] -> R[j] with cap = INF. Then we could find the minimal cut = maximal match of this graph = n — t.

    And the cut contains some of edges like (S->L[i]) and others like (R[i]->T). We collect all boy b such that (S->L[b]) is not removed. Then we know the neighborhood of these boys is all girl g such that (R[i]->T) is removed. And we could verify that |neig(b)| = |b| + t.

    → Reply