Hi. BOI (Baltic Olympiad in Informatics) will be held on Thursday and Friday. I just learnt that organizers provide possibility of participation in an online mirror of that contest. Enjoy: https://sio2.mimuw.edu.pl/en/c/boi2015-online/dashboard/ !
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
07:13:40
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
07:13:40
Зарегистрироваться »
*есть доп. регистрация
→ Трансляции
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 156 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.11.2024 10:21:20 (h2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











I would also be interested if they will provide live scoreboard of onsite event if you know.
I don't know anything about it, don't think that it will be published, but I don't exclude such possibility. But I guess that if sth like that will be available then there are 2 possible places. One is contest platform and second is fb fanpage https://www.facebook.com/boi.programming.contest?fref=ts
Check out Facebook profile:
https://www.facebook.com/boi.programming.contest
Why I can't submit practice problem ?!
"500 Internal Server Error" at the moment :(
I think we don't have full feedback ?!
Where can I find the results of online participants?
There is only a photo for results after 2.5 hours on the Facebook page
It's results of onsite participants. I asked for online ones.
The results will be available around 5PM CEST.
Will it be possible to practice the problems after the contest ends?
Can anyone share idea how to solve Tug of War? :)
Make a graph of 2n vertices that represent positions on the left and right rope segment respectively. Connect two vertices (representing different rope segments) with an edge of weight w if there exists a contestant of strength w who likes both positions on the rope.
It is easy to prove that if there exists a connected component which is a tree then solution does not exist. So let's check it at first.
So we get a graph that has 2n vertices, 2n edges and none of it's connected components is a tree. So it is a forest of medusas (trees with an additional edge that forms one cycle, looking as a cycle with trees attached to it's vertices). For every vertex of degree 1 we know how we have to assign the corresponding contestant, so iteratively remove those until only cycles are left.
Every cycle can be assigned to the left rope in only two ways, let's say one has cumulative strength A and the other B. We can at first use the strength A and leave the option to change the difference between cumulative strength of left and right rope segment by B - A for further use.
We can treat these options (B - A values) as items in knapsack problem and check if the solution exists this way.
It will not pass the time limit yet as the size of the knapsack is up to 20 * n and there are up to n items. However, we can see that the sum of the item values is also limited by 20 * n, so if there are a lot of items many of them will have the same value. Now we can group them in packages of size 2i (if we have 17 items of value 5 we split them into items of values [1, 2, 4, 8, 2]). It is easy to observe that the knapsack algorithm with these modified items produces exactly the same output as on the original ones, but is faster. That's the final algorithm and AFAIK it scores 100.
Finally let's adress what did I mean by "if there are a lot of items many of them will have the same value". Let's assume that there are m different values in the knapsack. So the sum of the items is at least 1 + 2 + ... + m = O(m2). As the sum is limited by 20·n then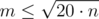 . So the complexity of the algoritm is
. So the complexity of the algoritm is 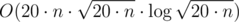 . I know that using 20 in this notation lacks the mind and dignity of a man, but I'm too lazy to correct it now.
. I know that using 20 in this notation lacks the mind and dignity of a man, but I'm too lazy to correct it now.
Ranking is now available !
I've been interested in why no one has decided Task: SEQ ???